Условие задачи:
Два одинаковых конденсатора соединены последовательно и подключены к источнику напряжения 12 В. На сколько изменится разность потенциалов на одном из конденсаторов, если другой погрузить в жидкость с диэлектрической проницаемостью 2?
Задача №6.4.30 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(U=12\) В, \(\varepsilon=2\), \(\Delta U-?\)
Решение задачи:
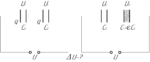 Пусть диэлектриком заполняется первый конденсатор, тогда нам необходимо найти изменение разности потенциалов в втором.
Пусть диэлектриком заполняется первый конденсатор, тогда нам необходимо найти изменение разности потенциалов в втором.
Изначально конденсаторы имели одинаковую емкость \(C_0\). Запишем формулу электроемкости для общего случая и выразим из этой формулы заряд \(q\):
\[C = \frac{q}{U}\]
\[q = CU\;\;\;\;(1)\]
Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый. Если воспользоваться формулой (1) и учесть тот факт, что конденсаторы имеют одинаковую емкость \(C_0\), то станет понятно, что напряжение на конденсаторах — одинаковое и равно некоторому \(U_1\). Также известно, что общее напряжение равно сумме напряжений на каждом из конденсаторов, поэтому:
\[U = {U_1} + {U_1}\]
\[U = 2{U_1}\]
\[{U_1} = \frac{U}{2}\;\;\;\;(2)\]
Далее первый конденсатор заполняют диэлектриком с диэлектрической проницаемостью \(\varepsilon\), отчего его емкость увеличивается и становится равной:
\[{C_1} = \varepsilon {C_0}\;\;\;\;(3)\]
Чтобы убедиться в достоверности этой формулы, Вам нужно записать формулу электроемкости плоского конденсатора.
Понятно, что напряжения на конденсаторах изменятся. Пусть теперь \(U_{11}\) — разность потенциалов между обкладками первого конденсатора, а \(U_2\) — разность потенциалов между обкладками второго. Проведя аналогичные рассуждения и пользуясь формулой (1), получим такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_{11}} = {C_0}{U_2} \hfill \\
U = {U_{11}} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим напряжение \(U_{11}\):
\[{U_{11}} = {U_2}\frac{{{C_0}}}{{{C_1}}}\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_2}\frac{{{C_0}}}{{{C_1}}} + {U_2}\]
\[U = {U_2}\frac{{{C_0} + {C_1}}}{{{C_1}}}\]
\[{U_2} = \frac{{U{C_1}}}{{{C_0} + {C_1}}}\]
Принимая во внимание выражение (3), получим:
\[{U_2} = \frac{{\varepsilon U{C_0}}}{{{C_0} + \varepsilon {C_0}}}\]
\[{U_2} = \frac{{\varepsilon U}}{{\varepsilon + 1}}\;\;\;\;(4)\]
Искомое изменение разности потенциалов \(\Delta U\), очевидно, будем искать по такой формуле (понятно, что \({U_2} > {U_1}\)):
\[\Delta U = {U_2} — {U_1}\;\;\;\;(5)\]
Осталось только подставить (2) и (4) в (5):
\[\Delta U = \frac{{\varepsilon U}}{{\varepsilon + 1}} — \frac{U}{2}\]
Приведем под общий знаменатель:
\[\Delta U = \frac{{2\varepsilon U — U\left( {\varepsilon + 1} \right)}}{{2\left( {\varepsilon + 1} \right)}}\]
Раскроем скобки в числителе:
\[\Delta U = \frac{{2\varepsilon U — \varepsilon U — U}}{{2\left( {\varepsilon + 1} \right)}}\]
\[\Delta U = \frac{{\varepsilon U — U}}{{2\left( {\varepsilon + 1} \right)}}\]
\[\Delta U = \frac{{U\left( {\varepsilon — 1} \right)}}{{2\left( {\varepsilon + 1} \right)}}\]
Отлично, задача решена, теперь посчитаем ответ:
\[\Delta U = \frac{{12 \cdot \left( {2 — 1} \right)}}{{2\left( {2 + 1} \right)}} = 2\;В\]
Ответ: 2 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.29 Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены
6.4.31 Бумага пробивается при напряженности поля 18 кВ/см. Два плоских конденсатора с изолятором
6.4.32 Три конденсатора электроемкостью 0,1, 0,125 и 0,5 мкФ соединены последовательно

 icodepro.ru
icodepro.ru
U=q\C тогда, чем больше С тем меньше U мы увеличили емкость второго конденсатора, значит напряжение на нем упало, тогда U2<U1.
Читайте внимательно решение: «Пусть диэлектриком заполняется первый конденсатор, тогда нам необходимо найти изменение разности потенциалов в втором»