icodepro.ruУсловие задачи:
Два одинаковых шара соединены тонкой трубкой, в которой находится капелька ртути, разделяющая шары. При 0° C капелька находится посередине трубки. Объем воздуха в каждом шаре и части трубки до капельки ртути равен 0,2 л. Площадь сечения трубки 200 мм2. На какое расстояние передвинется капелька, если один шар нагреть на 2° C, а другой на столько же охладить?
Задача №4.2.91 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=0^\circ\) C, \(V=0,2\) л, \(S=200\) мм2, \(\Delta t=2^\circ\) C, \(l-?\)
Решение задачи:
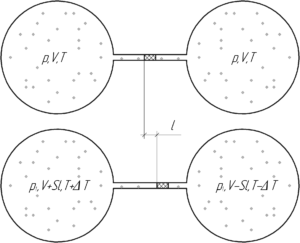Так как в начале воздух в обоих шарах занимает одинаковый объем, имеет одинаковую температуру и давление (поскольку капелька ртути не движется), значит в шарах находится одинаковое количество вещества воздуха \(\nu\).
Пусть после нагревания левого шара на величину \(\Delta T\) и охлаждения правого (на столько же) капелька ртути сместиться вправо на величину \(l\). Тогда объем, занимаемый воздухом в левом сосуде увеличится на величину \(Sl\), а в правом — уменьшится на эту величину. Давление воздуха в каждом сосуде будет одинаковым (иначе капелька бы двигалась), но возможно отличным от начального (нам это не интересно).
Запишем уравнение Клапейрона-Менделеева для конечного состояния воздуха в двух шарах:
\[\left\{ \begin{gathered}
{p_1}\left( {V + Sl} \right) = \nu R\left( {T + \Delta T} \right) \hfill \\
{p_1}\left( {V — Sl} \right) = \nu R\left( {T — \Delta T} \right) \hfill \\
\end{gathered} \right.\]
Поделим верхнее уравнение на нижнее, тогда:
\[\frac{{V + Sl}}{{V — Sl}} = \frac{{T + \Delta T}}{{T — \Delta T}}\]
Перемножим крест-накрест:
\[\left( {V + Sl} \right)\left( {T — \Delta T} \right) = \left( {V — Sl} \right)\left( {T + \Delta T} \right)\]
Раскроем скобки и выразим искомое перемещение \(l\):
\[VT — V\Delta T + SlT — Sl\Delta T = VT + V\Delta T — SlT — Sl\Delta T\]
\[2SlT = 2V\Delta T\]
\[l = \frac{{V\Delta T}}{{ST}}\]
Переведём исходные данные задачи в систему СИ:
\[0,2\;л = 0,2 \cdot {10^{ — 3}}\;м^3\]
\[2^\circ\;C = 2\;К\]
\[200\;мм^2 = 200 \cdot {10^{ — 6}}\;м^2\]
\[0^\circ\;C = 273\;К\]
Посчитаем численный ответ к задаче:
\[l = \frac{{0,2 \cdot {{10}^{ — 3}} \cdot 2}}{{200 \cdot {{10}^{ — 6}} \cdot 273}} = 7,33 \cdot {10^{ — 3}}\;м = 7,33\;мм\]
Ответ: 7,33 мм.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
4.2.90 Цилиндрический сосуд делится невесомым поршнем на две части. В одну часть сосуда
4.2.92 Внутри закрытого с обоих концов горизонтального цилиндра имеется тонкий поршень
4.2.93 Два одинаковых сосуда, содержащих газ при 300 К, соединили горизонтальной трубкой
Три одинаковых шара А, Б, В соединены трубками одинаковой длины и одинакового сечения (см. рисунок). Внутри трубок находятся капельки ртути, которые в исходном положении (при температуре T1) расположены посередине трубок. Объем воздуха в каждом шаре и части трубки до капельки ртути равен V1. Как передвинутся капельки, если шар Б нагреть на ?Т, а шар В – на 2?Т? Поперечное сечение трубок равно S.
Примечание: ?Т<<Т1; ввиду относительной малости изменений температуры и объема газа слагаемыми ?Тx?V можно пренебречь.
В результате нагревания объем газа в шаре А уменьшится на величину \(\Delta {V_1}\), объем газа в шаре В увеличится на величину \(\Delta {V_2}\), а объем газа в шаре Б изменится на величину \(\Delta {V_1} — \Delta {V_2}\). Давление газа во всех трех шарах после нагревания будет одинаковым и равным \(p\), поскольку капельки ртути будут находиться в равновесии. Запишем уравнения состояния газа для газов в каждом из шаров:\[\left\{ \begin{gathered}
\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{p\left( {{V_0} — \Delta {V_1}} \right)}}{{{T_0}}} \hfill \\
\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{p\left( {{V_0} + \Delta {V_1} — \Delta {V_2}} \right)}}{{{T_0} + \Delta T}} \hfill \\
\frac{{{p_0}{V_0}}}{{{T_0}}} = \frac{{p\left( {{V_0} + \Delta {V_2}} \right)}}{{{T_0} + 2\Delta T}} \hfill \\
\end{gathered} \right.\]Из 1-го и 3-го уравнений имеем:\[\frac{{{V_0} — \Delta {V_1}}}{{{T_0}}} = \frac{{{V_0} + \Delta {V_2}}}{{{T_0} + 2\Delta T}}\]Перемножаем «крест-накрест» и раскрываем скобки:\[\left( {{V_0} — \Delta {V_1}} \right)\left( {{T_0} + 2\Delta T} \right) = \left( {{V_0} + \Delta {V_2}} \right){T_0}\]\[{V_0}{T_0} + 2{V_0}\Delta T — \Delta {V_1}{T_0} — 2\Delta {V_1}\Delta T = {V_0}{T_0} + \Delta {V_2}{T_0}\]\[2{V_0}\Delta T — \Delta {V_1}{T_0} = \Delta {V_2}{T_0}\]\[2{V_0}\Delta T = {T_0}\left( {\Delta {V_1} + \Delta {V_2}} \right)\]Из 1-го и 2-го уравнений имеем:\[\frac{{{V_0} — \Delta {V_1}}}{{{T_0}}} = \frac{{{V_0} + \Delta {V_1} — \Delta {V_2}}}{{{T_0} + \Delta T}}\]Перемножаем «крест-накрест» и раскрываем скобки:\[{V_0}{T_0} + {V_0}\Delta T — \Delta {V_1}{T_0} — \Delta {V_1}\Delta T = {V_0}{T_0} + \Delta {V_1}{T_0} — \Delta {V_2}{T_0}\]\[{V_0}\Delta T — \Delta {V_1}{T_0} = \Delta {V_1}{T_0} — \Delta {V_2}{T_0}\]\[{V_0}\Delta T = {T_0}\left( {2\Delta {V_1} — \Delta {V_2}} \right)\]Имеем:\[\left\{ \begin{gathered}
2{V_0}\Delta T = {T_0}\left( {\Delta {V_1} + \Delta {V_2}} \right) \hfill \\
{V_0}\Delta T = {T_0}\left( {2\Delta {V_1} — \Delta {V_2}} \right) \hfill \\
\end{gathered} \right.\]Откуда:\[\Delta {V_1} + \Delta {V_2} = 4\Delta {V_1} — 2\Delta {V_2}\]\[3\Delta {V_2} = 3\Delta {V_1}\]\[\Delta {V_1} = \Delta {V_2}\]Получается, что объем среднего шара Б не изменится, поэтому каждая капелька ртути передвинется в сторону шара А на одну и ту же величину. Так как \(\Delta {V_1} = \Delta {V_2}\), то:\[{V_0}\Delta T = {T_0}\Delta {V_1}\]\[\Delta {V_1} = \frac{{{V_0}\Delta T}}{{{T_0}}}\]С другой стороны:\[\Delta {V_1} = S\Delta x\]Поэтому:\[\frac{{{V_0}\Delta T}}{{{T_0}}} = S\Delta x\]\[\Delta x = \frac{{{V_0}\Delta T}}{{S{T_0}}}\]
А почему 2 градуса по цельсию=2 градусам Кельвина
Потому что величина, которая равна двум градусам — это изменение температуры, а не абсолютная её величина.
Изменение температуры в обоих шкалах (имеется ввиду Цельсия и Кельвина) выражается одним и тем же числом. Например, вы нагрели воду на 100 C, значит вы ее на 100 К, согласны?