Условие задачи:

Два шарика с зарядами 0,8 и 0,5 мкКл находятся на расстоянии 0,4 м. До какого расстояния их можно сблизить, если совершить работу 27 мДж?

Задача №6.3.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(Q=0,8\) мкКл, \(q=0,5\) мкКл, \(R=0,4\) м, \(A=27\) мДж, \(r-?\)

Решение задачи:

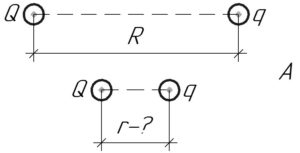Для того, чтобы сблизить два одноимённо заряженных шарика, необходимо совершить некоторой внешней силой положительную работу \(A\), поскольку потенциальная энергия системы из двух зарядов возрастёт (ведь она обратно пропорциональна расстоянию между зарядами, это видно далее из формулы). То есть запишем:

\[A = {W_2} — {W_1}\]

Здесь \(W_2\) — потенциальная энергия взаимодействия зарядов, когда их сблизят до искомого расстояния \(r\), \(W_1\) — начальная потенциальная энергия взаимодействия зарядов, когда они находятся на расстоянии \(R\). Значения этих потенциальных энергий можно найти из следующих формул:

\[\left\{ \begin{gathered}
{W_1} = \frac{{kQq}}{R} \hfill \\
{W_2} = \frac{{kQq}}{r} \hfill \\
\end{gathered} \right.\]

Сразу отметим, то здесь \(k\) — коэффициент пропорциональности (в законе Кулона), равный 9·10⁹ Н·м²/Кл².

Имеем:

\[A = \frac{{kQq}}{r} — \frac{{kQq}}{R}\]

Осталось только решить это уравнение с одним неизвестным.

\[\frac{{kQq}}{r} = A + \frac{{kQq}}{R}\]

\[\frac{{kQq}}{r} = \frac{{AR + kQq}}{R}\]

\[r = \frac{{kQqR}}{{AR + kQq}}\]

Задача решена в общем виде. Подставим численные значения в формулу, чтобы найти численный ответ.

\[r = \frac{{9 \cdot {{10}^9} \cdot 0,8 \cdot {{10}^{ — 6}} \cdot 0,5 \cdot {{10}^{ — 6}} \cdot 0,4}}{{27 \cdot {{10}^{ — 3}} \cdot 0,4 + 9 \cdot {{10}^9} \cdot 0,8 \cdot {{10}^{ — 6}} \cdot 0,5 \cdot {{10}^{ — 6}}}} = 0,1\;м\]

Ответ: 0,1 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.22 Электрическое поле в глицерине образовано точечным зарядом 9 нКл. Какую работу
6.3.24 Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности
6.3.25 Потенциал заряженного металлического шара 45 В. Какой минимальной скоростью