Условие задачи:

Два велосипедиста едут навстречу: один из них, имея скорость 7,2 км/ч, спускается с горы, разгоняется с ускорением 0,3 м/с²; другой, имея скорость 36 км/ч, поднимается замедленно с ускорением 0,2 м/с². Каково было расстояние между велосипедистами в начальный момент, если они встретились через 0,5 мин от начала движения?

Задача №1.3.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\upsilon_{01}=7,2\) км/ч, \(a_1=0,3\) м/с², \(\upsilon_{02}=36\) км/ч, \(a_2=0,2\) м/с², \(t=0,5\) мин, \(L-?\)

Решение задачи:

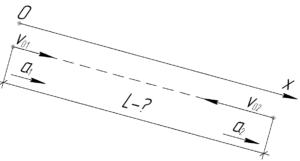Уравнение движения велосипедиста, спускающегося с горы с начальной скоростью \(\upsilon_{01}\) и ускорением \(a_1\), выглядит так:

\[{S_1}\left( t \right) = {\upsilon _{01}}t + \frac{{{a_1}{t^2}}}{2}\]

Уравнение движения другого, поднимающегося в гору с начальной скоростью \(\upsilon_{02}\) и замедлением \(a_2\), такое:

\[{S_2}\left( t \right) = {\upsilon _{02}}t — \frac{{{a_2}{t^2}}}{2}\]

Через время, равное \(t\), они встретятся, а значит пройдут в сумме искомое расстояние \(L\):

\[L = {S_1}\left( t \right) + {S_2}\left( t \right)\]

Подставим уравнения движения в последнее выражение:

\[L = {\upsilon _{01}}t + \frac{{{a_1}{t^2}}}{2} + {\upsilon _{02}}t — \frac{{{a_2}{t^2}}}{2}\]

\[L = \left( {{\upsilon _{01}} + {\upsilon _{02}}} \right)t + \frac{{\left( {{a_1} — {a_2}} \right){t^2}}}{2}\]

Все входящие в последнюю формулу величины нам известны. Переведем их численные значения в систему СИ, далее подставим в формулу и сосчитаем ответ.

\[7,2\; км/ч = \frac{{7,2 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{72}}{{36}}\; м/с = 2\; м/с\]

\[36\; км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{360}}{{36}}\; м/с = 10\; м/с\]

\[0,5\; мин = 0,5 \cdot 60\; с = 30\; с\]

\[L = \left( {2 + 10} \right) \cdot 30 + \frac{{\left( {0,3 — 0,2} \right) \cdot {{30}^2}}}{2} = 405\; м \approx 0,4\; км\]

Ответ: 0,4 км.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.3.42 Велосипедист начал свое движение из состояния покоя и в течение первых
1.3.44 За первую секунду равноускоренного движения тело проходит путь равный 1 м
1.3.45 По наклонной доске пустили снизу вверх шарик. На расстоянии 30 см от начала