Условие задачи:
Две трубки диаметром 4 см представляют собой сообщающиеся сосуды. В одно колено сосуда наливают 0,25 л воды, в другое — 0,25 л ртути. Какова будет разность уровней жидкости в коленах? Объемом изогнутой части трубки пренебречь.
Задача №3.1.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=4\) см, \(V_{в}=0,25\) л, \(V_{рт}=0,25\) л, \(\Delta h-?\)
Решение задачи:
\[\Delta h = {h_в} — {h_{рт}}\;\;\;\;(1)\]
Здесь \(h_{в}\) — это высота столба воды, а \(h_{рт}\) — это высота столба ртути, который уравновешивает столб воды.
Покажем на схеме горизонтальный уровень, ниже которого находится только ртуть. При равновесии давление жидкости на любом горизонтальном уровне одинаково (закон сообщающихся сосудов), поэтому:
\[{p_в} = {p_{рт}}\;\;\;\;(2)\]
Давление столба воды и ртути некоторой высоты можно найти по формулам:
\[\left\{ \begin{gathered}
{p_в} = {\rho _в}g{h_в} \hfill \\
{p_{рт}} = {\rho _{рт}}g{h_{рт}} \hfill \\
\end{gathered} \right.\]
Значит равенство (2) примет вид:
\[{\rho _в}g{h_в} = {\rho _{рт}}g{h_{рт}}\]
\[{h_{рт}} = \frac{{{\rho _в}{h_в}}}{{{\rho _{рт}}}}\;\;\;\;(3)\]
Так как сосуды цилиндрические, то высоту столба воды можно найти по формуле (площадь сечения цилиндра равна \(S = \frac{{\pi {d^2}}}{4}\)):
\[{h_в} = \frac{{4{V_в}}}{{\pi {d^2}}}\;\;\;\;(4)\]
Учитывая (3) и (4), формула (1) примет вид:
\[\Delta h = {h_в} — \frac{{{\rho _в}{h_в}}}{{{\rho _{рт}}}} = {h_в}\left( {1 — \frac{{{\rho _в}}}{{{\rho _{рт}}}}} \right)\]
\[\Delta h = \frac{{4{V_в}}}{{\pi {d^2}}}\left( {1 — \frac{{{\rho _в}}}{{{\rho _{рт}}}}} \right)\]
Переведем диаметр трубки и объем воды в систему СИ:
\[4\;см = 0,04\;м\]
\[0,25\;л = 0,25 \cdot {10^{ — 3}}\;м^3\]
Плотность воды равна 1000 кг/м3, плотность ртути — 13600 кг/м3. Считаем ответ:
\[\Delta h = \frac{{4 \cdot 0,25 \cdot {{10}^{ — 3}}}}{{3,14 \cdot {{0,04}^2}}}\left( {1 — \frac{{1000}}{{13600}}} \right) = 0,184\;м\]
Ответ: 0,184 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.1.40 В сообщающихся сосудах находится ртуть. Площадь сечения одного сосуда в 4 раза
3.1.42 Поршень весом 30 Н представляет собой круглый диск радиусом 4 см с отверстием
3.1.43 Определить массу груза, который можно поднять с помощью гидравлического поршня

 icodepro.ru
icodepro.ru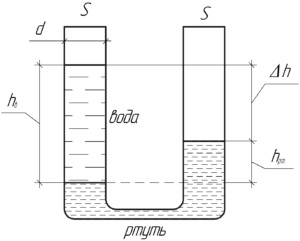
Помогите найти высоту наименьшего столба. Не получается с ответом, ответ: примерно 11 см
Скорее всего наименьшую высоту будет иметь столбик ртути, находящийся под столбиком воды. Так как в условии сказано, что объемом изогнутой части трубки можно пренебречь, то можем записать (так как по условию \({V_в} = {V_{рт}}\), далее у меня везде \(V\)):\[V = \frac{{\pi {d^2}}}{4}\left( {2{h_{\min }} + {h_{рт}}} \right)\]\[\frac{{4V}}{{\pi {d^2}}} = 2{h_{\min }} + {h_{рт}}\]Из формулы (3) вышеприведенного решения имеем:\[{h_{рт}} = \frac{{{\rho _в}{h_в}}}{{{\rho _{рт}}}}\]\[{h_{рт}} = \frac{{{\rho _в}}}{{{\rho _{рт}}}} \cdot \frac{{4V}}{{\pi {d^2}}}\]Тогда:\[\frac{{4V}}{{\pi {d^2}}} = 2{h_{\min }} + \frac{{{\rho _в}}}{{{\rho _{рт}}}} \cdot \frac{{4V}}{{\pi {d^2}}}\]\[\frac{{4V}}{{\pi {d^2}}}\left( {1 — \frac{{{\rho _в}}}{{{\rho _{рт}}}}} \right) = 2{h_{\min }}\]\[\frac{{4V}}{{\pi {d^2}}}\left( {\frac{{{\rho _{рт}} — {\rho _в}}}{{{\rho _{рт}}}}} \right) = 2{h_{\min }}\]\[{h_{\min }} = \frac{{2V}}{{\pi {d^2}}}\left( {\frac{{{\rho _{рт}} — {\rho _в}}}{{{\rho _{рт}}}}} \right)\]Численный ответ равен:\[{h_{\min }} = \frac{{2 \cdot 0,25 \cdot {{10}^{ — 3}}}}{{3,14 \cdot {{0,04}^2}}}\left( {\frac{{13600 — 1000}}{{13600}}} \right) = 0,092\;м = 9,2\;см\]
Хотел, что бы вы пересмотрели ваше решение, дайте мне надежду что я не совсем бездарь.(ответ не сходится)
Пересмотрел и ошибок не нашёл

Хоть напишите, какой ответ Вы получили, возможно я бы дал подсказку, где искать ошибку.
И вы не бездарь, Вы же пытаетесь, что-то делаете, а не просто списываете. Это дорогого стоит