Условие задачи:
Электрическое поле образовано двумя параллельными пластинами, находящимися на расстоянии 2 см друг от друга. Напряжение между ними 120 В. Какую скорость приобрел электрон под действием поля, пройдя из состояния покоя расстояние 3 мм по силовой линии?
Задача №6.3.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=2\) см, \(U=120\) В, \(\upsilon_0=0\) м/с, \(S=3\) мм, \(\upsilon-?\)
Решение задачи:
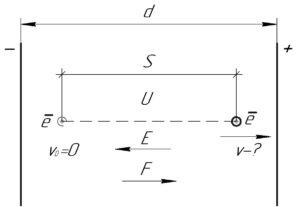 На электрон, находящийся в электрическом поле, действует электрическая сила \(F\), модуль которой мы определим таким образом:
На электрон, находящийся в электрическом поле, действует электрическая сила \(F\), модуль которой мы определим таким образом:
\[F = Ee\]
Здесь \(e\) — модуль заряда электрона (элементарный заряд), равный 1,6·10-19 Кл. Напряженность поля между пластинами \(E\) связана с напряжением \(U\) и расстоянием между пластинами \(d\) следующей формулой:
\[E = \frac{U}{d}\]
Тогда имеем:
\[F = \frac{{Ue}}{d}\]
Работу электрического поля \(A\) по перемещению заряда на расстояние \(S\) найдём так:
\[A = FS\]
\[A = \frac{{UeS}}{d}\;\;\;\;(1)\]
Также работу поля можно определить как изменение кинетической энергии электрона. Так как \(\upsilon_0=0\), то:
\[A = \frac{{{m_e}{\upsilon ^2}}}{2}\;\;\;\;(2)\]
Здесь \(m_e\) — масса электрона, равная 9,1·10-31 кг. Теперь приравняем (1) и (2), тогда получим:
\[\frac{{{m_e}{\upsilon ^2}}}{2} = \frac{{UeS}}{d}\]
Нам осталось только выразить искомую скорость \(\upsilon\):
\[\upsilon = \sqrt {\frac{{2UeS}}{{{m_e}d}}} \]
Произведём вычисления:
\[\upsilon = \sqrt {\frac{{2 \cdot 120 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 0,003}}{{9,1 \cdot {{10}^{ — 31}} \cdot 0,02}}} = 2,52 \cdot {10^6}\;м/с = 2520\;км/с\]
Ответ: 2520 км/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.38 Заряженная частица, пройдя ускоряющую разность потенциалов 600 кВ, приобрела
6.3.40 Пылинка массой 4×10^(-12) кг и зарядом 10^(-16) Кл попадает в поле заряженного
6.3.41 Пылинка массой 10 нг покоится в однородном электростатическом поле между

 icodepro.ru
icodepro.ru