Условие задачи:

Электрон влетает в плоский конденсатор параллельно его пластинам со скоростью 3000 км/с. Найти напряженность поля конденсатора, если электрон вылетает под углом 30° к пластинам. Длина пластины 20 см.

Задача №6.2.47 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon_0=3000$ км/с, $\alpha=30^\circ$, $l=20$ см, $E-?$

Решение задачи:

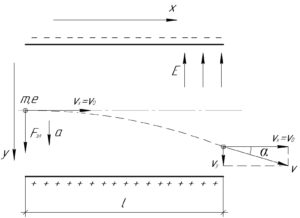Вдоль оси $y$ на электрон действует сила $F_{эл}$ со стороны электрического поля конденсатора напряженностью $E$, поэтому вдоль этой оси он будет двигаться ускоренно. Силу $F_{эл}$ можно найти по формуле:

$${F_{эл}} = Ee$$

Из второго закона Ньютона следует, что:

$${F_{эл}} = ma$$

В этих двух формулах $e$ — модуль заряда электрона, равный 1,6·10^-19 Кл, $m$ — масса электрона, равная 9,1·10^-31 кг. Тогда:

$$Ee = ma$$

$$E = \frac{{ma}}{e}\;\;\;\;(1)$$

Получается, что для нахождения напряженности $E$ нам нужно найти ускорение электрона $a$.

Запишем уравнения скорости электрона в проекциях на оси $x$ и $y$:

$$\left\{ \begin{gathered} ox:{\upsilon _x} = {\upsilon _0} \hfill \\ oy:{\upsilon _y} = at \hfill \\ \end{gathered} \right.$$

Поскольку вдоль оси $x$ электрон движется равномерно, то время движения $t$ электрона внутри конденсатора легко найти таким образом:

$$t = \frac{l}{{{\upsilon _0}}}$$

Тогда:

$$\left\{ \begin{gathered} ox:{\upsilon _x} = {\upsilon _0} \hfill \\ oy:{\upsilon _y} = \frac{{al}}{{{\upsilon _0}}} \hfill \\ \end{gathered} \right.$$

По условию электрон вылетает под углом $\alpha$ к пластинам. Из схемы видно, что:

$$tg\alpha = \frac{{{\upsilon _y}}}{{{\upsilon _x}}}$$

$$tg\alpha = \frac{{al}}{{\upsilon _0^2}}$$

Откуда ускорение $a$ равно:

$$a = \frac{{\upsilon _0^2 \cdot tg\alpha }}{l}$$

Для получения окончательной формулы подставим это выражение в формулу (1):

$$E = \frac{{m\upsilon _0^2 \cdot tg\alpha }}{{el}}$$

Численный ответ задачи равен:

$$E = \frac{{9,1 \cdot {{10}^{ — 31}} \cdot {{\left( {3 \cdot {{10}^6}} \right)}^2} \cdot tg30^\circ }}{{1,6 \cdot {{10}^{ — 19}} \cdot 0,2}} = 147,8\;В/м \approx 1,48\;В/см$$

Ответ: 1,48 В/см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.46 Протон движется с ускорением 76 км/с2 в электрическом поле. Определить
6.2.48 Электрон влетает в однородное электрическое поле напряженностью 200 В/м
6.2.49 Электрон, попадая в однородное электрическое поле, движется вдоль силовых линий