Условие задачи:
Батарея из двух последовательно соединенных конденсаторов электроемкостью 300 и 500 пФ заряжена до разности потенциалов 12 кВ. Определить разность потенциалов на первом конденсаторе.
Задача №6.4.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=300\) пФ, \(C_2=500\) пФ, \(U=12\) кВ, \(U_1-?\)
Решение задачи:
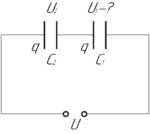 Для начала запишем формулу электроемкости и выразим из этой формулы заряд \(q\):
Для начала запишем формулу электроемкости и выразим из этой формулы заряд \(q\):
\[C = \frac{q}{U}\]
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) — разность потенциалов между обкладками первого конденсатора, а \(U_2\) — разность потенциалов между обкладками второго. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы получим такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим разность потенциалов \(U_2\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}}\]
\[U = {U_1}\frac{{{C_1} + {C_2}}}{{{C_2}}}\]
Откуда искомая разность потенциалов на первом конденсаторе \(U_1\) равна:
\[{U_1} = \frac{{U{C_2}}}{{{C_1} + {C_2}}}\]
Задача решена в общем виде, нам остается только посчитать ответ, для чего подставим данные задачи в полученную формулу, не забыв при этом перевести их в систему СИ:
\[{U_1} = \frac{{12 \cdot {{10}^3} \cdot 500 \cdot {{10}^{ — 12}}}}{{300 \cdot {{10}^{ — 12}} + 500 \cdot {{10}^{ — 12}}}} = 7500\;В\]
Ответ: 7500 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.24 Напряжение на батарее из двух последовательно включенных конденсаторов
6.4.26 Два последовательно соединенных конденсатора с электроемкостью 1 и 3 мкФ подключены
6.4.27 Два плоских конденсатора электроемкостью по 2 мкФ каждый, соединенные последовательно

 icodepro.ru
icodepro.ru