Условие задачи:

Два маленьких проводящих шарика подвешены на длинных непроводящих нитях к одному крючку. Шарики заряжены одинаковыми зарядами и находятся на расстоянии 5 см друг от друга. На каком расстоянии окажутся шарики, после того как один из них разрядить?

Задача №6.1.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(l=5\) см, \(L-?\)

Решение задачи:

Так как шарики с зарядом \(q\) каждый сначала находятся на расстоянии \(l\) друг от друга, то силу отталкивания между ними \(F_0\) можно найти из закона Кулона по такой формуле:

\[{F_0} = \frac{{k{q^2}}}{{{l^2}}}\;\;\;\;(1)\]

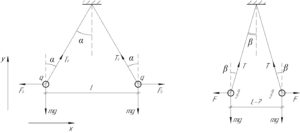
Изначально каждый из шариков будет находиться в равновесии под действием трёх сил: силы тяжести \(mg\), силы натяжения нити \(T_0\) и силы кулоновского отталкивания \(F_0\) (смотрите левую часть схемы к решению). Учитывая (1), запишем первый закон Ньютона в проекции на оси \(x\) и \(y\):

\[\left\{ \begin{gathered}
{T_0} \cdot \cos \alpha = mg \hfill \\
{T_0} \cdot \sin \alpha = \frac{{k{q^2}}}{{{l^2}}} \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство системы на верхнее, тогда получим:

\[tg\alpha = \frac{{k{q^2}}}{{mg{l^2}}}\;\;\;\;(2)\]

После того как один из шаров разрядят, между шарами исчезнет сила отталкивания, они придут в движении и, столкнувшись, разделят заряд \(q\) одного из шариков поровну (то есть теперь на каждом из шаров заряд равен \(\frac{q}{2}\)). Далее шары опять разойдутся так, что расстояние между ними станет равным \(L\) (смотрите правую часть схемы). Теперь сила отталкивания между шариками \(F\) по закону Кулона равна:

\[F = \frac{{k{q^2}}}{{4{L^2}}}\;\;\;\;(3)\]

Теперь на каждый шарик действуют три силы: сила тяжести \(mg\), сила натяжения нити \(T\) и сила кулоновского отталкивания \(F\). Шарики опять находятся в равновесии, поэтому, учитывая (3), опять запишем первый закон Ньютона в проекциях на оси координат:

\[\left\{ \begin{gathered}
T \cdot \cos \beta = mg \hfill \\
T \cdot \sin \beta = \frac{{k{q^2}}}{{4{L^2}}} \hfill \\
\end{gathered} \right.\]

Аналогично поделим нижнее равенство на верхнее:

\[tg\beta = \frac{{k{q^2}}}{{4mg{L^2}}}\;\;\;\;(4)\]

Теперь поделим (2) на (4):

\[\frac{{tg\alpha }}{{tg\beta }} = \frac{{k{q^2} \cdot 4mg{L^2}}}{{mg{l^2} \cdot k{q^2}}}\]

\[\frac{{tg\alpha }}{{tg\beta }} = \frac{{4{L^2}}}{{{l^2}}}\]

В условии сказано, что шарики подвешены на длинных нитях, значит углы \(\alpha\) и \(\beta\) — малые, поэтому справедливо равенство \(\sin \alpha \approx tg \alpha\) и \(\sin \beta \approx tg\beta\). Тогда:

\[\frac{{\sin \alpha }}{{\sin \beta }} = \frac{{4{L^2}}}{{{l^2}}}\]

Из рисунка понятно, что \(\sin \alpha = \frac{l}{2a}\) и \(\sin \beta = \frac{L}{2a}\) (здесь \(a\) — длина нити), значит:

\[\frac{{l \cdot 2a}}{{2a \cdot L}} = \frac{{4{L^2}}}{{{l^2}}}\]

\[\frac{l}{L} = \frac{{4{L^2}}}{{{l^2}}}\]

\[4{L^3} = {l^3}\]

\[L = \frac{l}{{\sqrt[3]{4}}}\]

Посчитаем ответ:

\[L = \frac{{0,05}}{{\sqrt[3]{4}}} = 0,031\;м\]

Ответ: 0,031 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.1.26 Два шарика массой по 1 г подвешены на нитях длиной 0,5 м в одной точке. После
6.1.28 Два одинаковых шарика, имеющих одинаковые заряды 1,6 мкКл, подвешены на одной
6.1.29 Точечные положительные заряды q и 2q закреплены на расстоянии L друг от друга