Решение: Два заряда по 25 нКл каждый, расположенные на расстоянии 0,24 м друг от друга

Условие задачи:

Два заряда по 25 нКл каждый, расположенные на расстоянии 0,24 м друг от друга, образуют электростатическое поле. С какой силой это поле действует на заряд 2 нКл, помещенный в точку, удалённую на 0,15 м от каждого из зарядов?

Задача №6.1.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$Q=25$ нКл, $R=0,24$ м, $q=2$ нКл, $r=0,15$ м, $F-?$

Решение задачи:

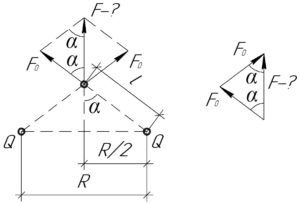Каждый из зарядов $Q$ действует на заряд $q$ с силой $F_0$ , которую можно определить из закона Кулона:

$F_0 = \frac{{kQq}}{{{r^2}}}\;\;\;\;(1)$

Тогда силу $F$ , с которой действуют оба заряда $Q$ (то есть с которой действует электростатическое поле) на заряд $q$ , найдём из принципа суперпозиции. Два вектора $F_0$ образуют равнобедренный треугольник, поэтому угол между ними равен $\left( {180^\circ — 2\alpha } \right)$ . Воспользуемся теоремой косинусов:

${F^2} = F_0^2 + F_0^2 — 2F_0^2 \cdot \cos \left( {180^\circ — 2\alpha } \right)$

$F = {F_0}\sqrt {2 — 2\cos \left( {180^\circ — 2\alpha } \right)} \;\;\;\;(2)$

Из тригонометрии известно, что:

$\cos \left( {180^\circ — 2\alpha } \right) = — \cos 2\alpha = — \left( {1 — 2{{\sin }^2}\alpha } \right) = 2{\sin ^2}\alpha — 1$

На схеме к решению видно, что:

$\sin \alpha = \frac{R}{{2r}}$

Поэтому:

$\cos \left( {180^\circ — 2\alpha } \right) = \frac{{2{R^2}}}{{4{r^2}}} — 1$

$\cos \left( {180^\circ — 2\alpha } \right) = \frac{{{R^2}}}{{2{r^2}}} — 1$

В таком случае формула (2) примет следующий вид:

$F = {F_0}\sqrt {2 — 2\left( {\frac{{{R^2}}}{{2{r^2}}} — 1} \right)} = {F_0}\sqrt {2 — \frac{{{R^2}}}{{{r^2}}} + 2}$

$F = {F_0}\sqrt {4 — \frac{{{R^2}}}{{{r^2}}}}$

Учитывая выражение (1), мы получим окончательную формулу:

$F = \frac{{kQq}}{{{r^2}}}\sqrt {4 — \frac{{{R^2}}}{{{r^2}}}}$

Посчитаем численный ответ:

$F = \frac{{9 \cdot {{10}^9} \cdot 25 \cdot {{10}^{ — 9}} \cdot 2 \cdot {{10}^{ — 9}}}}{{{{0,15}^2}}}\sqrt {4 — \frac{{{{0,24}^2}}}{{2 \cdot {{0,15}^2}}}} = 0,000024\;Н = 24\;мкН$