Условие задачи:
Две бесконечные плоскости, заряженные с поверхностной плотностью 2 и 0,6 мкКл/м2, пересекаются под прямым углом. С какой силой электрическое поле плоскостей действует на заряд 1 нКл, находящийся на биссектрисе угла между плоскостями?
Задача №6.2.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\sigma_1=2\) мкКл/м2, \(\sigma_2=0,6\) мкКл/м2, \(q=1\) нКл, \(F-?\)
Решение задачи:
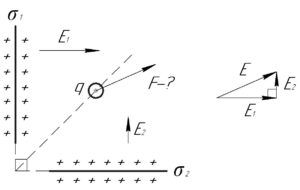 Каждая заряженная плоскость создаёт электрическое поле, модули напряженностей которых \(E_1\) и \(E_2\) можно определить по следующим формулам:
Каждая заряженная плоскость создаёт электрическое поле, модули напряженностей которых \(E_1\) и \(E_2\) можно определить по следующим формулам:
\[\left\{ \begin{gathered}
{E_1} = \frac{{{\sigma _1}}}{{2{\varepsilon _0}}} \hfill \\
{E_2} = \frac{{{\sigma _2}}}{{2{\varepsilon _0}}} \hfill \\
\end{gathered} \right.\]
Так как плоскости пересекаются под прямым углом, то результирующее электрическое поле двух пластин \(E\) можно найти как геометрическую сумму векторов напряженностей \(\overrightarrow {{E_1}}\) и \(\overrightarrow {{E_2}}\) по теореме Пифагора:
\[E = \sqrt {E_1^2 + E_2^2} \]
\[E = \sqrt {\frac{{\sigma _1^2}}{{4\varepsilon _0^2}} + \frac{{\sigma _2^2}}{{4\varepsilon _0^2}}} \]
\[E = \sqrt {\frac{{\sigma _1^2 + \sigma _2^2}}{{4\varepsilon _0^2}}} \]
Искомую же силу \(F\) определим так:
\[F = Eq\]
\[F = \sqrt {\frac{{\sigma _1^2 + \sigma _2^2}}{{4\varepsilon _0^2}}} q\]
\[F = \frac{q}{{2{\varepsilon _0}}}\sqrt {\sigma _1^2 + \sigma _2^2} \]
Задача решена, теперь произведём вычисления:
\[F = \frac{{{{10}^{ — 9}}}}{{2 \cdot 8,85 \cdot {{10}^{ — 12}}}}\sqrt {{{\left( {2 \cdot {{10}^{ — 6}}} \right)}^2} + {{\left( {0,6 \cdot {{10}^{ — 6}}} \right)}^2}} = 118 \cdot {10^{ — 6}}\;Н = 118\;мкН\]
Ответ: 118 мкН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.36 Две плоские пластинки площадью 200 см2, расстояние между которыми очень мало
6.2.38 Напряженность электрического поля вблизи земли перед разрядом молнии
6.2.39 Между горизонтальными пластинами заряженного конденсатора, напряженность

 icodepro.ru
icodepro.ru
4*pi*e0^2 можно было бы вынести из-под корня.
И в самом деле, но только без \(\pi^2\). Откорректировал, спасибо за замечание!