Условие задачи:
Электрическое поле в глицерине образовано точечным зарядом 9 нКл. Какую работу совершит поле, перемещая между точками, удаленными от этого заряда на 3 и 12 см, точечный заряд 5 нКл?
Задача №6.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(Q=9\) нКл, \(r_1=3\) см, \(r_2=12\) см, \(q=5\) нКл, \(A-?\)
Решение задачи:
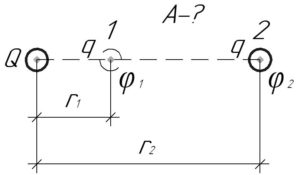 Работу электрического поля \(A\) точечного заряда \(Q\) можно определить как произведение разности потенциалов точек 1 и 2 \(\Delta \varphi\) (смотрите схему) на величину перемещаемого заряда \(q\):
Работу электрического поля \(A\) точечного заряда \(Q\) можно определить как произведение разности потенциалов точек 1 и 2 \(\Delta \varphi\) (смотрите схему) на величину перемещаемого заряда \(q\):
\[A = \Delta \varphi \cdot q\]
Разность потенциалов \(\Delta \varphi\) равна:
\[\Delta \varphi = {\varphi _1} — {\varphi _2}\]
Потенциалы электрического поля в точках 1 и 2 \(\varphi_1\) и \(\varphi_2\) легко найти по таким формулам:
\[\left\{ \begin{gathered}
{\varphi _1} = \frac{{kQ}}{{\varepsilon {r_1}}} \hfill \\
{\varphi _2} = \frac{{kQ}}{{\varepsilon {r_2}}} \hfill \\
\end{gathered} \right.\]
Здесь \(k\) — коэффициент пропорциональности, равный 9·109 Н·м2/Кл2, \(\varepsilon\) — диэлектрическая проницаемость глицерина, равная 39.
В итоге мы получим такое решение задачи в общем виде:
\[A = \frac{{kQq}}{{\varepsilon {r_1}}} — \frac{{kQq}}{{\varepsilon {r_2}}}\]
\[A = \frac{{kQq\left( {{r_2} — {r_1}} \right)}}{{\varepsilon {r_1}{r_2}}}\]
Посчитаем численное значение работы \(A\):
\[A = \frac{{9 \cdot {{10}^9} \cdot 9 \cdot {{10}^{ — 9}} \cdot 5 \cdot {{10}^{ — 9}} \cdot \left( {0,12 — 0,03} \right)}}{{39 \cdot 0,03 \cdot 0,12}} = 259,6 \cdot {10^{ — 9}}\;Дж \approx 260\;нДж\]
Ответ: 260 нДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.21 При лечении статическим душем к электродам электрической машины приложена
6.3.23 Два шарика с зарядами 0,8 и 0,5 мкКл находятся на расстоянии 0,4 м. До какого
6.3.24 Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности

 icodepro.ru
icodepro.ru
почему r1-r в числителе
ъ
я немного не пойму а работа домножена на перемещаемый заряд ?
Да, конечно, Вы разве не видите множитель q?