Электрон с некоторой скоростью влетает в плоский конденсатор параллельно

Условие задачи:

Электрон с некоторой скоростью влетает в плоский конденсатор параллельно пластинам на равном расстоянии от них. Напряжение на конденсаторе 300 В, длина пластин 10 см, расстояние между ними 2 см. При какой предельной скорости электрон не вылетит из конденсатора?

Задача №6.3.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(U=300\) В, \(l=10\) см, \(d=2\) см, \(\upsilon-?\)

Решение задачи:

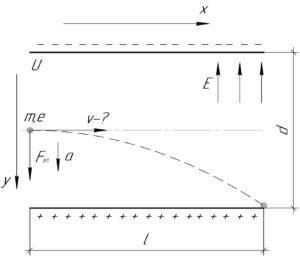На находящийся в поле плоского конденсатора электрон вдоль оси \(y\) действует электрическая сила \(F_{эл}\), модуль которой можно вычислить через напряженность поля конденсатора \(E\) и модуль заряда электрона \(e\) (он, между прочим, равен 1,6·10^-19 Кл):

\[{F_{эл}} = Ee\]

Напряженность поля конденсатора \(E\) связана с напряжением между обкладками \(U\) и расстоянием межу пластинами \(d\) по формуле:

\[E = \frac{U}{d}\]

Тогда получим:

\[{F_{эл}} = \frac{{Ue}}{d}\;\;\;\;(1)\]

Запишем второй закон Ньютона для электрона в проекции на ось \(y\):

\[{F_{эл}} = ma\]

Здесь \(m\) – масса электрона, равная 9,1·10^-31 кг. Учитывая формулу (1), имеем:

\[\frac{{Ue}}{d} = ma\]

\[a = \frac{{Ue}}{{md}}\;\;\;\;(2)\]

Отлично, мы нашли ускорение электрона вдоль оси \(y\). Давайте запишем уравнения движения электрона вдоль обеих осей координат. Понятно, что вдоль оси \(x\) электрон движется равномерно с некоторой скоростью \(\upsilon\), а вдоль оси \(y\) равноускоренно с ускорением \(a\).

\[\left\{ \begin{gathered}
x = \upsilon t \hfill \\
y = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]

Теперь, чтобы найти предельную скорость (наибольшую, при которой электрон ещё не вылетает из конденсатора), рассмотрим крайний случай, когда электрон попадаёт в край нижней обкладки (смотрите рисунок). Тогда \(x=l\), \(y=\frac{d}{2}\), и система примет вид:

\[\left\{ \begin{gathered}
l = \upsilon t \hfill \\
\frac{d}{2} = \frac{{a{t^2}}}{2} \hfill \\
\end{gathered} \right.\]

Принимая во внимание формулу (2), получим:

\[\left\{ \begin{gathered}
l = \upsilon t \hfill \\
d = \frac{{Ue{t^2}}}{{md}} \hfill \\
\end{gathered} \right.\]

Из нижнего равенства системы выразим время движения \(t\):

\[t = \sqrt {\frac{{m{d^2}}}{{Ue}}} \]

Из верхнего равенства получим:

\[\upsilon = \frac{l}{t}\]

В итоге мы получим следующее решение задачи в общем виде:

\[\upsilon = l\sqrt {\frac{{Ue}}{{m{d^2}}}} \]

\[\upsilon = \frac{l}{d}\sqrt {\frac{{Ue}}{m}} \]

Численно предельная скорость \(\upsilon\) равна:

\[\upsilon = \frac{{0,1}}{{0,02}}\sqrt {\frac{{300 \cdot 1,6 \cdot {{10}^{ – 19}}}}{{9,1 \cdot {{10}^{ – 31}}}}} = 36,3 \cdot {10^6}\;м/с = 36,3\;Мм/с\]

При скорости ниже указанной электрон не будет вылетать из конденсатора, т.е. будет сталкиваться с обкладкой конденсатора.

Ответ: 36,3 Мм/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.41 Пылинка массой 10 нг покоится в однородном электростатическом поле между
6.3.43 Какую разность потенциалов должен пройти первоначально покоящийся электрон
6.3.44 Какую скорость может сообщить электрону, находящемуся в состоянии покоя