Условие задачи:
Капля массой 10-13 кг поднимается вертикально вверх с ускорением 2,2 м/с2 между пластинами горизонтального плоского конденсатора. Найти заряд капли, если поверхностная плотность заряда на пластина равна 6,6 мкКл/м2.
Задача №6.2.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10^{-13}\) кг, \(a=2,2\) м/с2, \(\sigma=6,6\) мкКл/м2, \(q-?\)
Решение задачи:
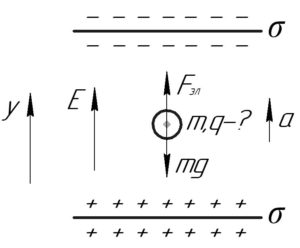 На каплю действуют сила тяжести \(mg\) и сила взаимодействия со стороны электрического поля конденсатора \(F_{эл}\). Под действием указанных двух сил капля движется равноускоренно вверх, поэтому запишем второй закон Ньютона в проекции на ось \(y\):
На каплю действуют сила тяжести \(mg\) и сила взаимодействия со стороны электрического поля конденсатора \(F_{эл}\). Под действием указанных двух сил капля движется равноускоренно вверх, поэтому запишем второй закон Ньютона в проекции на ось \(y\):
\[{F_{эл}} — mg = ma\;\;\;\;(1)\]
Силу \(F_{эл}\), действующую на каплю с искомым зарядом \(q\) со стороны электрического поля конденсатора, можно определить по такой известной формуле:
\[{F_{эл}} = Eq\]
Напряженность электрического поля воздушного конденсатора \(E\) равна:
\[E = \frac{\sigma }{{{\varepsilon _0}}}\]
Здесь \(\varepsilon _0\) — электрическая постоянная, равная 8,85·10-12 Ф/м. Тогда:
\[{F_{эл}} = \frac{{\sigma q}}{{{\varepsilon _0}}}\]
В итоге формула (1) примет такой вид:
\[\frac{{\sigma q}}{{{\varepsilon _0}}} — mg = ma\]
\[\frac{{\sigma q}}{{{\varepsilon _0}}} = m\left( {a + g} \right)\]
\[q = \frac{{m\left( {a + g} \right){\varepsilon _0}}}{\sigma }\]
Задача решена в общем виде, теперь произведём расчёт численного ответа (не забываем переводить значения величин в систему СИ):
\[q = \frac{{{{10}^{ — 13}} \cdot \left( {2,2 + 9,8} \right) \cdot 8,85 \cdot {{10}^{ — 12}}}}{{6,6 \cdot {{10}^{ — 6}}}} = 160 \cdot {10^{ — 20}}\;Кл\]
Заряд капли положителен и равен 10 элементарным зарядам.
Ответ: 160·10-20 Кл.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.41 Капля массой 10^(-10) г, на которой находится заряд, равный 10 зарядам электрона
6.2.43 Положительно заряженный шарик массой 18 г и плотностью 1800 кг/м3 находится
6.2.44 Для ионизации нейтральной молекулы воздуха электрон должен обладать

 icodepro.ru
icodepro.ru