Условие задачи:
Найти потенциал электрического поля в точке, лежащей посредине между двумя зарядами по 50 нКл, расположенными на расстоянии 1 м в вакууме.
Задача №6.3.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q=50\) нКл, \(r=\frac{l}{2}\), \(l=1\) м, \(\varphi-?\)
Решение задачи:
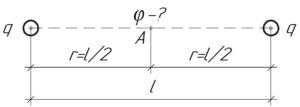 Так как заряды одинаковы, и они находятся на одинаковом расстоянии \(r\) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
Так как заряды одинаковы, и они находятся на одинаковом расстоянии \(r\) от точки A, в которой нужно определить потенциал, значит потенциалы электрических полей в точке A, создаваемых каждым зарядом, также одинаковы. Это видно из формулы:
\[{\varphi _0} = \frac{{kq}}{r}\]
Здесь \(k\) — коэффициент пропорциональности, равный 9·109 Н·м2/Кл2.
Учитывая, что точка A находится посредине между двумя зарядами (\(r=\frac{l}{2}\)), то:
\[{\varphi _0} = \frac{{2kq}}{l}\]
Искомый потенциал \(\varphi\) равен сумме потенциалов электрических полей в точке A, создаваемых каждым зарядом, поскольку потенциал — величина скалярная. Учитывая вышесказанное, имеем:
\[\varphi = {\varphi _0} + {\varphi _0}\]
\[\varphi = 2{\varphi _0}\]
В итоге решение задачи в общем виде выглядит так:
\[\varphi = \frac{{4kq}}{l}\]
Произведём вычисления:
\[\varphi = \frac{{4 \cdot 9 \cdot {{10}^9} \cdot 50 \cdot {{10}^{ — 9}}}}{1} = 1800\;В = 1,8\;кВ\]
Ответ: 1,8 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими

 icodepro.ru
icodepro.ru