icodepro.ruУсловие задачи:
Напряжение на батарее из двух последовательно включенных конденсаторов электроемкостью 20 и 30 мкФ равно 1 кВ. Чему равна разность напряжений на первом и втором конденсаторе?
Задача №6.4.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(C_1=20\) мкФ, \(C_2=30\) мкФ, \(U=1\) кВ, \(\Delta U-?\)
Решение задачи:
Для начала запишем формулу электроемкости:
\[C = \frac{q}{U}\]
Выразим из этой формулы заряд \(q\):
\[q = CU\;\;\;\;(1)\]
Пусть \(U_1\) – напряжение между обкладками первого конденсатора, а \(U_2\) – напряжение между обкладками второго. Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый, а общее напряжение равно сумме напряжений на каждом из конденсаторов. Учитывая все написанное и пользуясь формулой (1), мы можем получить такую систему:
\[\left\{ \begin{gathered}
{C_1}{U_1} = {C_2}{U_2} \hfill \\
U = {U_1} + {U_2} \hfill \\
\end{gathered} \right.\]
Из верхнего равенства системы выразим напряжение \(U_2\):
\[{U_2} = {U_1}\frac{{{C_1}}}{{{C_2}}}\;\;\;\;(2)\]
Полученное выражение подставим в нижнее равенство системы:
\[U = {U_1} + {U_1}\frac{{{C_1}}}{{{C_2}}}\]
\[U = {U_1}\frac{{{C_1} + {C_2}}}{{{C_2}}}\]
Откуда напряжение на первом конденсаторе \(U_1\) равно:
\[{U_1} = \frac{{U{C_2}}}{{{C_1} + {C_2}}}\;\;\;\;(3)\]
Используя формулу (2), найдем напряжение на втором конденсаторе \(U_2\):
\[{U_2} = \frac{{U{C_2}}}{{{C_1} + {C_2}}} \cdot \frac{{{C_1}}}{{{C_2}}}\]
\[{U_2} = \frac{{U{C_1}}}{{{C_1} + {C_2}}}\;\;\;\;(4)\]
Так как из данных задачи видно, что \({C_2} > {C_1}\), то из формул (3) и (4) видно, что \({U_1} > {U_2}\), поэтому искомую разность напряжений \(\Delta U\) будем искать по формуле:
\[\Delta U = {U_1} – {U_2}\]
Используя выражения (3) и (4), получим:
\[\Delta U = \frac{{U{C_2}}}{{{C_1} + {C_2}}} – \frac{{U{C_1}}}{{{C_1} + {C_2}}}\]
\[\Delta U = \frac{{U\left( {{C_2} – {C_1}} \right)}}{{{C_1} + {C_2}}}\]
Задача решена, остается только посчитать ответ:
\[\Delta U = \frac{{1000 \cdot \left( {30 \cdot {{10}^{ – 6}} – 20 \cdot {{10}^{ – 6}}} \right)}}{{20 \cdot {{10}^{ – 6}} + 30 \cdot {{10}^{ – 6}}}} = 200\;В = 0,2\;кВ\]
Ответ: 0,2 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.4.23 Две пластины конденсатора площадью 2 дм2 находятся в керосине на расстоянии 4 мм
6.4.25 Батарея из двух последовательно соединенных конденсаторов электроемкостью
6.4.26 Два последовательно соединенных конденсатора с электроемкостью 1 и 3 мкФ подключены
“Известно, что при последовательном соединении конденсаторов заряд на их обкладках одинаковый” – почему?
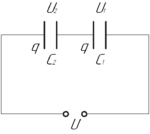
Объясню следующим образом. Пронумеруем обкладки двух конденсаторов, изображенных на рисунке к задаче, слева направо (1-2-3-4). Пусть изначально конденсаторы не заряжены, из этого следует, что суммарный заряд обкладок 2 и 3, которые соединены между собой, равен нулю (да и вообще заряд всех обкладок равен 0). Далее на батарею подаётся напряжение, в цепи начинает течь ток. Допустим, что на обкладку 1 притечет заряд q. Тогда очевидно, что заряд обкладки 2 станет равным -q. А вот заряд обкладки 3 станет равным q, чтобы сумма зарядов обкладок 2 и 3 осталась равным 0.
Если объяснять коротко, то при последовательном соединении конденсаторов заряд на их обкладках одинаковый из-за того, что на соединенных пластинах заряд равен нулю.
Объясните пожалуйста, откуда берётся напряжение между двумя соединёнными последовательно конденсаторами, если между обкладками диэлектрик и напряжение не должно попадать на следующий конденсатор при подаче постоянного питания.
Если диэлектрик не проводит ток, это ещё не значит, что диэлектрик не проводит электрическое поле. Когда на цепь конденсаторов подают напряжение, происходит перераспределение зарядов на обкладках (см. комментарий выше), поэтому между обкладками будет возникать электрическое поле, а значит, и напряжение.