Условие задачи:
Неподвижно закрепленный шарик, заряженный положительно, находится над шариком, заряженным отрицательно. Заряды шариков одинаковы, масса каждого равна 0,01 г, радиус 1 мм и расстояние между центрами шаров 20 мм. Какой должна быть их разность потенциалов, чтобы верхний шарик мог поднять нижний.
Задача №6.3.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=0,01\) г, \(R=1\) мм, \(l=20\) мм, \(\Delta \varphi-?\)
Решение задачи:
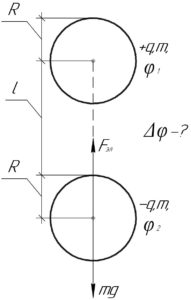 Чтобы верхний шарик смог поднять нижний, в начальный момент электрическая сила \(F_{эл}\), действующая на нижний шарик, должна быть больше силы тяжести \(mg\), то есть:
Чтобы верхний шарик смог поднять нижний, в начальный момент электрическая сила \(F_{эл}\), действующая на нижний шарик, должна быть больше силы тяжести \(mg\), то есть:
\[{F_{эл}} > mg\]
Если это условие выполняется, то нижний шарик будет двигаться вверх с ускорением, расстояние между шарами со временем будет уменьшаться, из-за чего сила \(F_{эл}\) будет возрастать (поскольку она обратно пропорциональна расстоянию) — то есть нижний шарик будет двигаться с переменным ускорением. В принципе мы можем рассмотреть и случай равенства сил, в таком случае любой сколь угодно малый толчок нижнего шарика вверх приведёт к такому же исходу. Поэтому:
\[{F_{эл}} = mg\]
Распишем силу электрического взаимодействия по известной формуле, тогда:
\[\frac{{k{q^2}}}{{{l^2}}} = mg\]
Откуда неизвестный модуль заряда шариков \(q\) равен:
\[q = \sqrt {\frac{{mg{l^2}}}{k}} = l\sqrt {\frac{{mg}}{k}} \;\;\;\;(1)\]
Всем известно, что потенциал заряженных шариков можно найти по формулам (\(\varphi_1\) — верхний шарик, \(\varphi_2\) — нижний шарик):
\[\left\{ \begin{gathered}
{\varphi _1} = \frac{{kq}}{R} \hfill \\
{\varphi _2} = \frac{{ — kq}}{R} \hfill \\
\end{gathered} \right.\]
Искомую разность потенциалов \(\Delta \varphi\), очевидно, нужно искать таким образом:
\[\Delta \varphi = {\varphi _1} — {\varphi _2}\]
Тогда:
\[\Delta \varphi = \frac{{kq}}{R} — \left( { — \frac{{kq}}{R}} \right)\]
\[\Delta \varphi = \frac{{2kq}}{R}\]
Теперь в эту формулу подставим выражение (1):
\[\Delta \varphi = \frac{{2kl}}{R}\sqrt {\frac{{mg}}{k}} \]
\[\Delta \varphi = \frac{{2l}}{R}\sqrt {mgk} \]
Вуаля, задача решена в общем виде. Подставим в эту формулу численные значения величин в системе СИ:
\[\Delta \varphi = \frac{{2 \cdot 0,02}}{{0,001}}\sqrt {0,01 \cdot {{10}^{ — 3}} \cdot 10 \cdot 9 \cdot {{10}^9}} = 37947,3\;В \approx 38\;кВ\]
Ответ: 38 кВ.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.55 В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед
6.3.57 Заряды q1=2 мкКл и q2=5 мкКл расположены на расстоянии AB=40 см друг от друга
6.3.58 Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см

 icodepro.ru
icodepro.ru