Решение: Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если

Условие задачи:

Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если напряженность поля в точке, находящейся на середине этого расстояния, равна 550 В/м.

Задача №6.2.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q_1=16\) нКл, \(q_2=-6\) нКл, \(r=\frac{l}{2}\), \(E=550\) В/м, \(l-?\)

Решение задачи:

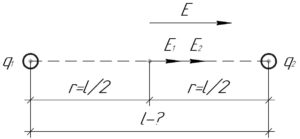Модули напряженностей электрических полей \(E_1\) и \(E_2\) от зарядов \(q_1\) и \(q_2\) соответственно на расстоянии \(r\) от каждого из них найдём по таким формулам:

\[\left\{ \begin{gathered}
{E_1} = \frac{{k{q_1}}}{{{r^2}}} \hfill \\
{E_2} = \frac{{k\left| {{q_2}} \right|}}{{{r^2}}} \hfill \\
\end{gathered} \right.\]

Здесь \(k\) – коэффициент пропорциональности (в законе Кулона), равный 9·10⁹ Н·м²/Кл².

Учитывая тот факт, что по условию \(r=\frac{l}{2}\), и раскрывая модуль в нижней формуле (\( \left| {{q_2}} \right| = – {q_2}\) ), получим:

\[\left\{ \begin{gathered}
{E_1} = \frac{{4k{q_1}}}{{{l^2}}} \hfill \\
{E_2} = \frac{{ – 4k{q_2}}}{{{l^2}}} \hfill \\
\end{gathered} \right.\]

На схеме к решению видно, что напряженности полей \(E_1\) и \(E_2\) сонаправлены, поэтому:

\[E = {E_1} + {E_2}\]

\[E = \frac{{4k{q_1}}}{{{l^2}}} + \frac{{ – 4k{q_2}}}{{{l^2}}}\]

\[E = \frac{{4k}}{{{l^2}}}\left( {{q_1} – {q_2}} \right)\]

Откуда искомое расстояние между зарядами \(l\) равно:

\[l = \sqrt {\frac{{4k\left( {{q_1} – {q_2}} \right)}}{E}} \]

Посчитаем численный ответ:

\[l = \sqrt {\frac{{4 \cdot 9 \cdot {{10}^9} \cdot \left( {16 \cdot {{10}^{ – 9}} – \left( { – 6 \cdot {{10}^{ – 9}}} \right)} \right)}}{{550}}} = 1,2\;м = 120\;см\]