Условие задачи:
Поле равномерно заряженной плоскости действует в вакууме на заряд 0,2 нКл с силой 22,6 мкН. Какова поверхностная плотность заряда на пластине?
Задача №6.2.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(q=0,2\) нКл, \(F=22,6\) мкН, \(\sigma-?\)
Решение задачи:
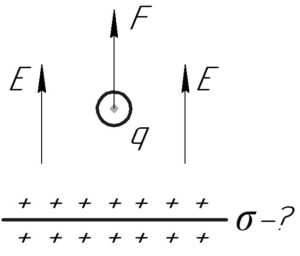 Силу \(F\), действующую на заряд \(q\) со стороны электрического поля пластины, напряженность которого \(E\), можно найти по такой формуле:
Силу \(F\), действующую на заряд \(q\) со стороны электрического поля пластины, напряженность которого \(E\), можно найти по такой формуле:
\[F = Eq\;\;\;\;(1)\]
Напряженность поля \(E\) равномерно заряженной пластины определим по такой формуле (её можно вывести из теоремы Гаусса):
\[E = \frac{\sigma }{{2{\varepsilon _0}}}\;\;\;\;(2)\]
Здесь \(\sigma\) – искомая поверхностная плотность заряда пластины, \(\varepsilon _0\) – электрическая постоянная, равная 8,85·10-12 Ф/м.
Подставим выражение (2) в формулу (1), получим:
\[F = \frac{{\sigma q}}{{2{\varepsilon _0}}}\]
Откуда поверхностная плотность заряда на пластине \(\sigma\) равна:
\[\sigma = \frac{{2F{\varepsilon _0}}}{q}\]
Посчитаем численный ответ:
\[\sigma = \frac{{2 \cdot 22,6 \cdot {{10}^{ – 6}} \cdot 8,85 \cdot {{10}^{ – 12}}}}{{0,2 \cdot {{10}^{ – 9}}}} = 2 \cdot {10^{ – 6}}\;Кл/м^2 = 2\;мкКл/м^2\]
Ответ: 2 мкКл/м2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.2.32 В однородном электрическом поле напряженностью 1 МВ/м, направленном вверх
6.2.34 Бесконечная, равномерно заряженная пластина имеет поверхностную плотность
6.2.35 Две бесконечные параллельные пластины равномерно заряжены поверхностной

 icodepro.ru
icodepro.ru