Условие задачи:

Проводящий шар радиуса \(R\) заряжен зарядом \(q\). Найти напряженность поля в точке на расстоянии \(\frac{R}{2}\) от центра шара.

Задача №6.2.57 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R\), \(q\), \(l=\frac{R}{2}\), \(E-?\)

Решение задачи:

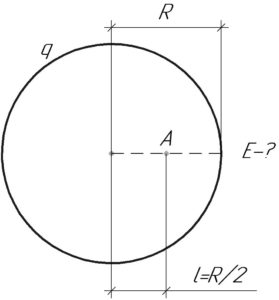Так как расстояние \(l\), равное \(\frac{R}{2}\), меньше чем радиус шара \(R\), значит указанная точка (точка A) находится внутри шара (смотрите схему). Известно, что напряженность поля в любой точке внутри заряженного шара равна нулю. Доказать это строго можно с помощью теоремы Гаусса.

\[E = 0\;В/м\]

Ответ: 0 В/м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.2.56 Равномерно заряженный проводящий шар радиуса 5 см создаёт на расстоянии 10 см
6.2.58 Точечный отрицательный заряд создаёт на расстоянии 10 см поле, напряженность
6.3.1 Указать размерность единицы потенциала электростатического поля