Решение: Пылинка массой 10 нг покоится в однородном электростатическом поле между

Условие задачи:

Пылинка массой 10 нг покоится в однородном электростатическом поле между пластинами конденсатора с разностью потенциалов между ними 6 кВ и расстоянием 6 см. Какое надо приложить напряжение к пластинам, чтобы пылинка осталась в равновесии, потеряв заряд, равный заряду 4000 электронов? Электрическое поле направлено вертикально вверх.

Задача №6.3.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) нг, \(\Delta \varphi_1=6\) кВ, \(d=6\) см, \(\Delta q=4000e\), \(\Delta \varphi_2-?\)

Решение задачи:

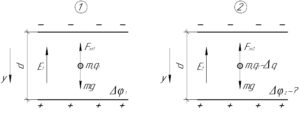Для начала нужно провести некоторые разъяснения. Вполне очевидно, что электрическая сила, действующая на пылинку, направлена вверх, иначе она не могла бы находиться в равновесии (смотрите схему). Так как поле направлено вертикально вверх, получается, что пылинка имеет положительный заряд. Также фраза “потеряв заряд, равный заряду 4000 электронов” означает, что заряд пылинки уменьшится, она никак не эквивалента фразе “пылинку покинуло 4000 электронов”, поэтому справедливо соотношение:

\[{q_2} = {q_1} – \Delta q\]

Запишем первый закон Ньютона в проекции на ось \(y\) для случая 1 (т.е. до потери заряда, смотрите схему справа):

\[mg = {F_{эл1}}\;\;\;\;(1)\]

Электрическую силу \(F_{эл1}\) можно найти через напряженность поля \(E_1\) и заряд пылинки \(q\) по формуле:

\[{F_{эл1}} = {E_1}{q_1}\]

Напряженность поля \(E_1\) связана с разностью потенциалов между пластинами \(\Delta \varphi_1\) и расстоянием между ними \(d\) следующим образом:

\[{E_1} = \frac{{\Delta {\varphi _1}}}{d}\]

Тогда формула (1) примет такой вид:

\[mg = \frac{{\Delta {\varphi _1}{q_1}}}{d}\]

Сразу выразим из полученного равенства неизвестный начальный заряд пылинки \(q_1\):

\[{q_1} = \frac{{mgd}}{{\Delta {\varphi _1}}}\;\;\;\;(2)\]

Чтобы удержать пылинку в равновесии после потери ею заряда, необходимо увеличить разность потенциалов на пластинах (это повлечёт за собой увеличение напряженности электрического поля). Теперь выполняя аналогичные рассуждения, запишем первый закон Ньютона для случая 2 (после потери заряда):

\[mg = \frac{{\Delta {\varphi _2}}}{d}\left( {{q_1} – \Delta q} \right)\]

Учитывая (2), имеем:

\[mg = \frac{{\Delta {\varphi _2}}}{d}\left( {\frac{{mgd}}{{\Delta {\varphi _1}}} – \Delta q} \right)\]

\[mg = \Delta {\varphi _2}\left( {\frac{{mg}}{{\Delta {\varphi _1}}} – \frac{{\Delta q}}{d}} \right)\]

В правой части в скобках приведём под общий знаменатель:

\[mg = \Delta {\varphi _2}\left( {\frac{{mgd – \Delta q\Delta {\varphi _1}}}{{\Delta {\varphi _1}d}}} \right)\]

Выразим искомую разность потенциалов \(\Delta \varphi_2\):

\[\Delta {\varphi _2} = \frac{{mg\Delta {\varphi _1}d}}{{mgd – \Delta q\Delta {\varphi _1}}}\]

Принимая во внимание тот факт, что по условию \(\Delta q=4000e\), где \(e\) – элементарный заряд, равный 1,6·10^-19 Кл, мы получим такое решение задачи в общем виде:

\[\Delta {\varphi _2} = \frac{{mg\Delta {\varphi _1}d}}{{mgd – 4000e\Delta {\varphi _1}}}\]

Произведём расчёт численного ответа задачи:

\[\Delta {\varphi _2} = \frac{{10 \cdot {{10}^{ – 12}} \cdot 10 \cdot 6 \cdot {{10}^3} \cdot 0,06}}{{10 \cdot {{10}^{ – 12}} \cdot 10 \cdot 0,06 – 4000 \cdot 1,6 \cdot {{10}^{ – 19}} \cdot 6 \cdot {{10}^3}}} = 16666,7\;В\]