Три одинаковых конденсатора соединены, как показано на рисунке. При

Условие задачи:

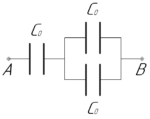Три одинаковых конденсатора соединены, как показано на рисунке. При разности потенциалов между точками A и B в 1000 В энергия батареи конденсаторов равна 2 Дж. Найти емкость каждого конденсатора.

Задача №6.4.66 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(U=1000\) В, \(W=2\) Дж, \(C_0-?\)

Решение задачи:

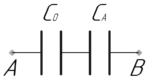Мы видим, что два конденсатора одинаковой емкости \(C_0\) соединены параллельно, их эквивалентная емкость \(C_A\) равна:

\[{C_A} = 2{C_0}\;\;\;\;(1)\]

В таком случае вся батарея состоит их двух последовательно соединенных конденсаторов \(C_A\) и \(C_0\), поэтому электроемкость всей батареи \(C\) равна:

\[\frac{1}{C} = \frac{1}{{{C_A}}} + \frac{1}{{{C_0}}}\]

Учитывая (1), получим:

\[\frac{1}{C} = \frac{1}{{2{C_0}}} + \frac{1}{{{C_0}}}\]

\[\frac{1}{C} = \frac{1}{{2{C_0}}} + \frac{2}{{2{C_0}}}\]

\[\frac{1}{C} = \frac{3}{{2{C_0}}}\]

\[C = \frac{{2{C_0}}}{3}\;\;\;\;(1)\]

Энергию \(W\), накопленную в батарее конденсаторов, определяют по формуле:

\[W = \frac{{C{U^2}}}{2}\]

Подставим в эту формулу выражение (2), тогда получим:

\[W = \frac{{{C_0}{U^2}}}{3}\]

Откуда искомая электроемкость одного конденсатора \(C_0\) равна:

\[{C_0} = \frac{{3W}}{{{U^2}}}\]

Произведем расчет численного ответа:

\[{C_0} = \frac{{3 \cdot 2}}{{{{1000}^2}}} = 6 \cdot {10^{ – 6}}\;Ф = 6\;мкФ\]

Ответ: 6 мкФ.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.4.65 Три одинаковых конденсатора соединены, как показано на рисунке. При разности
6.4.67 Три одинаковых конденсатора соединены, как показано на рисунке. При разности потенциалов
6.4.68 Площадь каждой пластины плоского вакуумного конденсатора S. Конденсатор заряжен