Решение: В однородном электрическом поле напряженностью 1 МВ/м, направленном вверх

Условие задачи:

В однородном электрическом поле напряженностью 1 МВ/м, направленном вверх под углом 30° к вертикали, висит на нити шарик массой 2 г с зарядом 10 нКл. Найти силу натяжения нити.

Задача №6.2.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(E=1\) МВ/м, \(\alpha=30^\circ\), \(m=2\) г, \(q=10\) нКл, \(T-?\)

Решение задачи:

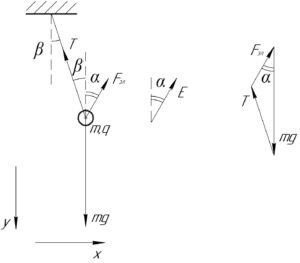Шарик находится в равновесии под действием трёх сил: силы тяжести \(mg\), силы натяжения нити \(T\) и электрической силы \(F_{эл}\), действующей на шарик со стороны электрического поля (смотрите схему). Запишем первый закон Ньютона в векторной форме:

\[m\overrightarrow g + \overrightarrow T + \overrightarrow {{F_{эл}}} = \overrightarrow 0\;\;\;\;(1)\]

Электрическую силу \(F_{эл}\) можно определить по такой формуле:

\[{F_{эл}} = Eq\]

Тогда равенство (1) примет вид:

\[m\overrightarrow g + \overrightarrow T + \overrightarrow E q = \overrightarrow 0 \]

Это векторное равенство графически можно представить в виде векторного треугольника (смотрите правую часть схему). Тогда применим теорему косинусов:

\[{T^2} = {E^2}{q^2} + {m^2}{g^2} – 2Eqmg \cdot \cos \alpha \]

\[T = \sqrt {{E^2}{q^2} + {m^2}{g^2} – 2Eqmg \cdot \cos \alpha } \]

Задача решена в общем виде, посчитаем численный ответ:

\[T = \sqrt {{{10}^{12}} \cdot {{\left( {10 \cdot {{10}^{ – 9}}} \right)}^2} + {{\left( {2 \cdot {{10}^{ – 3}}} \right)}^2} \cdot {{10}^2} – 2 \cdot {{10}^6} \cdot 10 \cdot {{10}^{ – 9}} \cdot 2 \cdot {{10}^{ – 3}} \cdot 10 \cdot \cos 30^\circ } = 0,0124\;Н\]

Это наиболее короткое решение этой задачи.