Условие задачи:
Игрок посылает мяч с высоты \(h=1,2\) м над землей так, что угол бросания 45°. На расстоянии \(S=47\) м от места бросания расположена сетка высотой \(H=7,3\) м. Какова должна быть минимальная скорость, чтобы мяч перескочил сетку?
Задача №1.6.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(h=1,2\) м, \(\alpha=45^\circ\), \(S=47\) м, \(H=7,3\) м, \(v_0-?\)
Решение задачи:
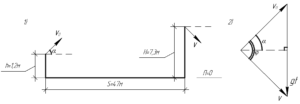 Представленная задача имеет высокий уровень сложности, и несмотря на простое условие, решается нетривиально. Здесь необходимы методы решения задач по кинематике, которые отличаются от тех, которые мы применяли ранее. Ранее мы всегда полагались на аналитические методы, т.е. всегда решали различные уравнения в проекциях. В этой задаче мы будем использовать векторный метод решения задач на кинематику. Рисунок к задаче приведен, как всегда, справа.
Представленная задача имеет высокий уровень сложности, и несмотря на простое условие, решается нетривиально. Здесь необходимы методы решения задач по кинематике, которые отличаются от тех, которые мы применяли ранее. Ранее мы всегда полагались на аналитические методы, т.е. всегда решали различные уравнения в проекциях. В этой задаче мы будем использовать векторный метод решения задач на кинематику. Рисунок к задаче приведен, как всегда, справа.
Большинство людей думают, что мяч перескочит сетку при минимальной скорости при броске, если в точке над сеткой у мяча будет наивысшая точка подъема, т.е. отсутствовать вертикальная составляющая скорости. Ни черта подобного! Но давайте сначала найдем зависимость между скоростью бросания и скоростью над сеткой, использую закон сохранения энергии (ЗСЭ), нуль потенциальной энергии выбран на уровне земли (смотрите часть рисунка под номером (1)):
\[\frac{{mv_0^2}}{2} + mgh = \frac{{m{v^2}}}{2} + mgH\]
Сократив обе части уравнения на \(m\), получим:
\[{v^2} = v_0^2 — 2g(H — h)\]
\[v = \sqrt {v_0^2 — 2g(H — h)} \]
Теперь взглянем на наш рисунок, точнее на его вторую часть. Угол \(\varphi\) — это угол между векторами скоростей \(v_0\) и \(v\). Здесь изображен треугольник скоростей, который олицетворяет векторное уравнение:
\[\overrightarrow v = \overrightarrow {{v_0}} + \overrightarrow g t\]
Заметим, что его площадь можно найти двумя способами — через половину произведение сторон и синус угла между ними и через половину произведения основания на высоту:
\[{S_\Delta } = \frac{1}{2}v{v_0}\sin \varphi = \frac{1}{2}gt{v_{0x}}\]
Учитывая, что \(S = {v_{0x}}t\), имеем:
\[v{v_0}\sin \varphi = Sg\]
\[v{v_0} = \frac{{Sg}}{{\sin \varphi }}\]
Подставим полученную ранее нами формулу для определения \(v\) через \(v_0\).
\[{v_0}\sqrt {v_0^2 — 2g(H — h)} = \frac{{Sg}}{{\sin \varphi }}\]
Теперь поразмыслим над этой формулой.
Очень важно понять следующее. Если мы ищем минимальную начальную скорость, то левая часть приведенного выше уравнения должна принимать минимальное значение (т.к. вы остальные величины постоянные и заданы условием). Тогда и правая часть уравнения должна быть минимальной, а это возможно лишь при максимальном значении синуса угла, т.е. при \(\sin \varphi = 1\) или \(\varphi = 90^\circ \).
Значит:
\[{v_0}\sqrt {v_0^2 — 2g(H — h)} = Sg\]
Дальнейшее решение этой непростой задачи сводится к решению этого уравнения. Возведем обе его части в квадрат:
\[v_0^2\left( {v_0^2 — 2g(H — h)} \right) = S^2g^2\]
Произведем замену \(u = v_0^2\), тогда:
\[u\left( {u — 2g(H — h)} \right) = S^2g^2\]
\[{u^2} — 2g(H — h)u — S^2g^2 = 0\]
\[D = 4{g^2}{(H — h)^2} + 4S^2g^2\]
\[u = \frac{{2g(H — h) \pm \sqrt {4{g^2}{{(H — h)}^2} + 4S^2g^2} }}{2}\]
\[u = g(H — h) \pm \sqrt {{g^2}{{(H — h)}^2} + S^2g^2} \]
Видно, что корень со знаком «минус» получается отрицательным, отбрасываем его:
\[u = g(H — h) + \sqrt {{g^2}{{(H — h)}^2} + S^2g^2} \]
Производя обратную замену, получаем:
\[{v_0} = \sqrt {g(H — h) + \sqrt {{g^2}{{(H — h)}^2} + S^2g^2} } \]
Подставим все исходные данные в системе измерения СИ и получим численный ответ:
\[{v_0} = \sqrt {10(7,3 — 1,2) + \sqrt {{{10}^2}{{(7,3 — 1,2)}^2} + 47^2 \cdot 10^2} } = 23,13\; м/с = 83,26\; км/ч\]
Ответ: 83,26 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.13 Бомбардировщик пикирует на цель под углом 60 градусов к горизонту
1.6.15 Камень, брошенный под углом к горизонту, упал на землю
1.6.16 Из орудия сделан выстрел вверх по склону горы. Угол наклона горы

 icodepro.ru
icodepro.ru
Очень плохо, что ваше решение выпадает первым. В результате у детей взрывается могз. Задача решается намного проще:
h = h0+voy*(L/vox)-g(L/vox)^2 /2
h = h0+Ltga-gL^2 /2(vocosa))^2
откуда легко находится vo!
В задаче указаны все данные для получения траектории тела, которое вылетает под определенным углом (да еще и под 45 градусов)…
x = V0*cos(a)*t
y = V0*sin(a) — g*t^2/2
или
47 = V0 * sqrt(2)/2 * t
7.3 — 1.2 = V0*sqrt(2)/2*t — 10 * t^2 / 2
или
6.1 = 47 — 5 * t^2
t = 6.39 (c)
V0 = 10.4 (м/с)
и ни о какой минимальной скорости и речи нет…
Если вычислять угол, при котором скорость д.б. минимальной, то это совсем другая задача…
Опечатка
x = V0*cos(a)*t
y = y0 + V0*sin(a)*t – g*t^2/2
Почему высота будет проекцией начальной скорости на ось х?
strannaia zadacha! reshil bi tak: reshenie identicno zadache N 1.6.9 OX; S= Vo*cos45*t, ——> t= S/Vo*cos45 ;
OY: H-h=Vo*sin45*t — g*t*t/2
uchtem cchto: Vo*sin45*t=Vo*cos45t=S cos45*cos45=2/4,
reshim sistemu. poluchim: Vo*Vo=g*S*S/(S-H+h) ——> Vo =23 m/c, totje otvet, chto u vas. esli g=9.8 m/c*c . i esli g=10m/c*c Vo=23.24 m/c
dalshe khuje; analizuia rezultat iasno, preodelenie dannoi ((H-h) ot OX) visoti proiskhodit posle prokhojdenia h(max), t. e. vo vtorom polovine poleta , vremia poleta na rastoianie S=47m -2.92 c.
vremia do padena na OX,(polni polet do OX)— 3.28 c. (uroven OX na visote h paralelno zemli ) pri otvete: Vo=23.13m/c, i danni ugol 45; cto-to ne poluChaetsia preodalet visotu (H-h) OX proxodit na visote h.
Bolshim uvajeniem, Gocha.
Да, я усложнил решение задачи, её можно было решить Вашим способом. Каюсь!
Но есть одно большое «но», я бы даже сказал огромное «но». Ваше решение возможно из-за того, что в задаче дан угол бросания \(\alpha\), в олимпиадной версии этой задачи его нет, поэтому решить олимпиадную версию Вы уже не сможете.
Если Вам интересно, вот её текст:
«С какой минимальной скоростью и под каким углом к горизонту следует бросить камень с горизонтальной поверхности земли, чтобы он смог перелететь через тонкую стену высотой \(h\)? Точка бросания находится на расстоянии \(L\) от стены. Ускорение свободного падения \(g\). Сопротивлением воздуха пренебречь.»
Хм, с цифрами действительно что-то не так, мне нужно перепроверить решение, дополню свой ответ позже.
UPD:
Угол броска, при котором необходимая для преодоления преграды скорость будет минимальна, определяют по формуле (применительно к данной задаче):\[\alpha = arctg\left( {\frac{{{\upsilon _0}}}{{\sqrt {\upsilon _0^2 + 2g\left( {H — h} \right)} }}} \right)\]Произведем вычисления:\[\alpha = arctg\left( {\frac{{23,13}}{{\sqrt {{{23,13}^2} + 2 \cdot 10 \cdot \left( {7,3 — 1,2} \right)} }}} \right) = 42,06^\circ \]Как Вы видите, угол отличается от того, что дан нам в условии, поэтому текущее решение неверное, нужно решать так, как это делаете Вы (чуть позже я переделаю решение).
Спасибо Вам за Ваши комментарии, они очень ценные и помогают развивать ресурс.
Почему В думаете, что решить олимпиадную задачу нельзя?
Странно…
1) Выражайте
V=V(alpha)
или наоборот
alpha = alpha(V)
2) Берите производную…
3) …а дальше все понятно…
a esli tak : 1.vichislim vremia poleta do setki po os OX. S=Vocos *t. i postavim vo (2)
2, po osi OY, ( H-h)=Vosin*t-gt2/2.
doljno poluchitsia proshche.
Нам же неизвестна начальная скорость, как Вы время собираетесь найти?

Это непростая задача. Я так понимаю, Вы просто прочитали условие и мое решение и решили, что её можно решить проще. Но попробуйте решить её сами, это далеко не так просто, как Вам кажется
Там решение гораздо проше, в пять действий.
Конечная формула: (((g*S^2)/2(S-H+h))^0.5)/sin a
Где это — там?
Почему отбросили корень со знаком минус? Ничего в этом такого, вот если минус был внутри — тогда стоило бы задуматься(но тут совсем другой случай)
Все понял принял) Там подразумевался корень которого еще нет..
И всё-таки, можно ли решить эту задачу более компактным способом?
Судя по громоздкому ответу — нет, я знаю только еще более длинный способ решения с обилием математики
Кажется разобралась. Спасибо)
Только вот получается не 23,13 м/с, а 23,057 м/с. Вы, видимо, как-то округляли до большего.
Разница не так критична
Ни черта не понял постараюсь ещё раз прочитать)
Эта очень сложная задача, возможно придётся перечитать не один раз. А вообще ещё лучше, если Вы повторите решение и логические рассуждения.
Вы очень хорошо решаете задачи, доступно излагаете ход решения и умело используете математический аппарат

Спасибо