Условие задачи:
К валу, радиус которого 5 см, прикреплена нить. Через 5 с после начала равномерного вращения вала на него намоталось 10 м нити. Чему равны период и угловая скорость вращения вала?
Задача №1.8.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
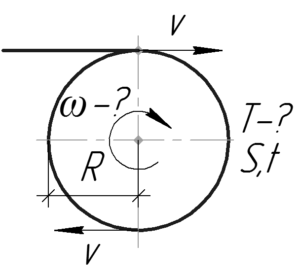
\(R=5\) см, \(t=5\) с, \(S=10\) м, \(T-?\), \(\omega-?\)
Решение задачи:
 Период, то есть время, за которое делается полный оборот вала, найдем, разделив все время \(t\) на количество оборотов \(N\).
Период, то есть время, за которое делается полный оборот вала, найдем, разделив все время \(t\) на количество оборотов \(N\).
\[T = \frac{t}{N}\]
Любая точка вала прошла по окружности за все время путь \(S\). Так как периметр окружности легко найти из формулы \(2\pi R\), то легко найти количество оборотов \(N\).
\[N = \frac{S}{{2\pi R}}\]
В итоге период найдем по такой формуле:
\[T = \frac{{2\pi Rt}}{S}\]
Угловая скорость связана с периодом соотношением:
\[\omega = \frac{{2\pi }}{T}\]
Подставим в это выражение полученную нами ранее формулу для периода. Не забываем переводить все подставляемые величины в систему СИ.
\[\omega = \frac{{2\pi S}}{{2\pi Rt}} = \frac{S}{{Rt}}\]
Осталось только посчитать ответы.
\[T = \frac{{2 \cdot 3,14 \cdot 0,05 \cdot 5}}{{10}} = 0,16\; с\]
\[\omega = \frac{{10}}{{0,05 \cdot 5}} = 40\; рад/с\]
Ответ: 0,16 с; 40 рад/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.14 Тепловоз движется со скоростью 60 км/ч. Сколько оборотов в секунду делают его
1.8.16 Велосипедист начинает двигаться делать поворот по кругу со скоростью 10 м/с
1.8.17 Вертолет начал снижаться вертикально вниз с ускорением 0,2 м/с2. Лопасть винта

 icodepro.ru
icodepro.ru
можете S=20 м и R=5 метров
А время какое? Если \(t=5\) с, то:\[\omega = \frac{{20}}{{5 \cdot 5}} = 0,8\;рад/с\]
Эту задачу можно решить через линейную скорость? Т.е. v=S/t, затем подставляем в формулу для нахождения угловой скорости w=v/R и имеем w=s/tR. А дальше находим период по формуле T=2п/w
Разумеется, так тоже будет правильно
Здорово, но вы забыли определить частоту вращения вала.
Мы решили задачу в том виде, в каком она была дана в указанном выше сборнике.
Если Вы используете другой сборник, то вероятно Вам указано найти и частоту вращения вала. Думаю, это не должно составить трудности, поскольку мы уже знаем период, а частота есть величина обратная периоду.