Условие задачи:

Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности в точку, находящуюся на расстоянии 1 см от поверхности шара радиусом 1 см с поверхностной плотностью заряда 1 нКл/см².

Задача №6.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$q=20$ нКл, $r_1=\infty$, $r_2=1$ см, $R=1$ см, $\sigma=1$ нКл/см², $A-?$

Решение задачи:

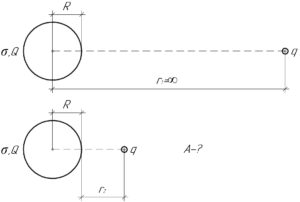Во-первых, нужно понимать, что для сближения двух одноимённо заряженных тел необходимо совершить внешней силой положительную работу, так как потенциальная энергия взаимодействия зарядов увеличивается при сближении. Очевидно, что:

$$A = {W_2} — {W_1}$$

Здесь $W_1$ — начальная потенциальная энергия взаимодействия зарядов, а $W_2$ — конечная. Их легко определить по таким известным формулам:

$$\left\{ \begin{gathered} {W_1} = \frac{{kQq}}{{{r_1}}} \hfill \\ {W_2} = \frac{{kQq}}{{R + {r_2}}} \hfill \\ \end{gathered} \right.$$

Здесь $k$ — коэффициент пропорциональности (из закона Кулона), равный 9·10⁹ Н·м²/Кл², а $Q$ — заряд шара, который можно выразить через площадь поверхности шара $S$ и поверхностную плотность заряда $\sigma$ по формуле:

$$Q = \sigma \cdot S$$

$$Q = \sigma \cdot 4\pi {R^2}$$

Так как $r_1=\infty$, то понятно, что $W_1=0$.

В итоге мы получим такую окончательную формулу:

$$A = \frac{{4\pi kq\sigma {R^2}}}{{R + {r_2}}}$$

Численное значение работы $A$ равно:

$$A = \frac{{4 \cdot 3,14 \cdot 9 \cdot {{10}^9} \cdot 20 \cdot {{10}^{ — 9}} \cdot 1 \cdot {{10}^{ — 5}} \cdot {{0,01}^2}}}{{0,01 + 0,01}} = 113 \cdot {10^{ — 6}} \;Дж = 113\;мкДж$$

Ответ: 113 мкДж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.3.23 Два шарика с зарядами 0,8 и 0,5 мкКл находятся на расстоянии 0,4 м. До какого
6.3.25 Потенциал заряженного металлического шара 45 В. Какой минимальной скоростью
6.3.26 Две равномерно заряженные проводящие пластины образовали однородное поле