Условие задачи:

Какой скоростью обладал мальчик при прыжке с трамплина, находящегося на горе с уклоном 45°, если он приземлился на склоне горы на расстоянии 29 м от трамплина, покинув его в горизонтальном направлении?

Задача №1.6.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\alpha=45^\circ$, $L=29$ м, $v_0-?$

Решение задачи:

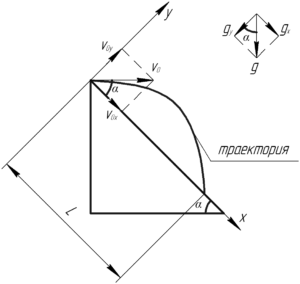Как и в этой задаче для решения необходимо ввести оси $x$ и $y$, по склону горы и перпендикулярно ему соответственно (см. рисунок, для увеличения кликните мышью).

Заметим, что при данном направлении осей, необходимо проецировать и вектор ускорения свободного падения $g$, что обычно в простых задачах кинематики не делается, т.к. направление оси $x$ обычно выбирается перпендикулярным направлению вектора $g$.

Дальнейшее решение в принципе тривиально, достаточно лишь записать уравнения движения мальчика в проекциях на введенные оси.

$$\left\{ \begin{gathered} ox:x = {v_0}\cos \alpha \cdot t + \frac{{g \cdot \sin \alpha {t^2}}}{2}\,\,\,(1) \hfill \\ oy:y = {v_0}\sin \alpha \cdot t — \frac{{g \cdot \cos \alpha {t^2}}}{2}\,\,(2) \hfill \\ \end{gathered} \right.$$

Время прыжка, т.е. время от момента прыжка до прикосновения со склоном, можно найти из уравнения (2) и условия:

$$y = 0 \Rightarrow {v_0}\sin \alpha  \cdot t — \frac{{g \cdot \cos \alpha {t^2}}}{2} = 0$$

$$\left[ \begin{gathered} t = 0 \hfill \\ t = \frac{{2{v_0}\sin \alpha }}{{g\cos \alpha }} \hfill \\ \end{gathered} \right.$$

Получаем два корня, один из которых соответствует моменту отрыва от трамплина. Второй корень подставляем в уравнение (1) и получаем:

$$L = \frac{{2v_0^2\sin \alpha }}{g} + \frac{{2v_0^2{{\sin }^3}\alpha }}{{g{{\cos }^2}\alpha }} = v_0^2\frac{{2\sin \alpha  \cdot {{\cos }^2}\alpha  + 2{{\sin }^3}\alpha }}{{g{{\cos }^2}\alpha }}$$

Выражаем из уравнения $v_0$ и получаем ответ в общем виде:

$${v_0} = \cos \alpha \sqrt {\frac{{Lg}}{{2\sin \alpha  \cdot {{\cos }^2}\alpha  + 2{{\sin }^3}\alpha }}}$$

Подставляя значение из данных задачи, получаем ответ:

$${v_0} = \cos 45^\circ \sqrt {\frac{{29 \cdot 10}}{{2\sin 45^\circ  \cdot {{\cos }^2}45^\circ  + 2{{\sin }^3}45^\circ }}}  = 10,13\; м/с = 36,45\; км/ч$$

Ответ: 36,45 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.18 Какое расстояние по горизонтали до первого удара о пол
1.6.20 С вершины холма бросают камень с начальной скоростью
1.6.21 Струя воды бьет под углом 32 градуса к горизонту. На расстоянии