Условие задачи:
Камень брошен под углом 30° к горизонту. Кинетическая энергия камня в верхней точке траектории 45 Дж. Чему равна в этой точке потенциальная энергия камня?
Задача №2.7.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=30^\circ\), \(E_{к}=45\) Дж, \(E_п-?\)
Решение задачи:
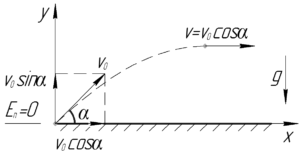 Так как сопротивление воздуха отсутствует, то согласно закону сохранения энергии:
Так как сопротивление воздуха отсутствует, то согласно закону сохранения энергии:
\[{E_{к0}} = {E_к} + {E_п}\]
Здесь \(E_{к0}\) — начальная кинетическая энергия, а \(E_к\) и \(E_п\)— соответственно кинетическая и потенциальная энергии в верхней точке траектории.
Значит:
\[{E_п} = {E_{к0}} — {E_к}\;\;\;\;(1)\]
Понятно, что скорость камня в верхней точке равна проекции начальной скорости \(\upsilon_0\) на ось \(x\):
\[\upsilon = {\upsilon _0}\cos \alpha \]
Тогда:
\[{E_{к0}} = \frac{{m\upsilon _0^2}}{2}\]
\[{E_к} = \frac{{m\upsilon _0^2{{\cos }^2}\alpha }}{2}\;\;\;\;(2)\]
Формула (1) примет вид:
\[{E_п} = \frac{{m\upsilon _0^2}}{2} — \frac{{m\upsilon _0^2{{\cos }^2}\alpha }}{2} = \frac{{m\upsilon _0^2}}{2}\left( {1 — {{\cos }^2}\alpha } \right)\]
Согласно основному тригонометрическому тождеству \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), поэтому \(1 — {\cos ^2}\alpha = {\sin ^2}\alpha\). Значит:
\[{E_п} = \frac{{m\upsilon _0^2{{\sin }^2}\alpha }}{2}\]
Домножим и поделим дробь на \({\cos ^2}\alpha\):
\[{E_п} = \frac{{m\upsilon _0^2{{\sin }^2}\alpha }}{2} \cdot \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\]
Принимая во внимание равенство (2), получим:
\[{E_п} = {E_к} \cdot \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = {E_к} \cdot t{g^2}\alpha \]
Посчитаем ответ:
\[{E_п} = 45 \cdot t{g^2}30^\circ = 15\;Дж\]
Ответ: 15 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.7.26 Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой
2.7.28 Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с
2.7.29 На тело массой 10 кг действует постоянная сила 5 Н. Определить кинетическую энергию

 icodepro.ru
icodepro.ru
Спасибо за помощь в подготовке!