Условие задачи:

Канат может выдержать нагрузку 2,5 кН. С каким максимальным ускорением можно поднимать груз массой 200 кг, чтобы канат не разорвался?

Задача №2.1.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$T_{max}=2,5$ кН, $m=200$ кг, $a_{max}-?$

Решение задачи:

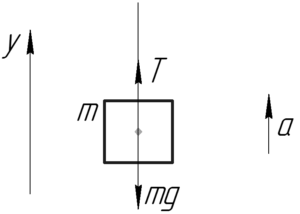На схеме показан груз, на который действуют всего две силы: сила тяжести $mg$ и сила натяжения каната $T$. Так как груз движется с ускорением, то воспользуемся вторым законом Ньютона в проекции на ось $y$.

$$T — mg = ma$$

Выразим ускорение $a$.

$$a = \frac{{T — mg}}{m}$$

Почленно разделим числитель на знаменатель:

$$a = \frac{T}{m} — \frac{{mg}}{m}$$

$$a = \frac{T}{m} — g$$

Так определяется ускорение в общем случае. Когда ускорение станет таким, что канат будет готов разорваться, то его сила натяжения $T$ станет равной максимальной нагрузке $T_{max}$.

$$a_{max} = \frac{{{T_{max}}}}{m} — g$$

В итоге мы получили решение задачи в общем виде. Остается только посчитать ответ.

$$a_{max} = \frac{{2,5 \cdot {{10}^3}}}{{200}} — 10 = 2,5\; м/с^2$$

Ответ: 2,5 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.33 Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.36 Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см