icodepro.ruУсловие задачи:
Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На какое расстояние будет снесен катер течением, если скорость течения 1,5 м/с?
Задача №1.7.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=600\) м, \(\upsilon_1=4\) м/с, \(\upsilon_0=1,5\) м/с, \(L-?\)
Решение задачи:
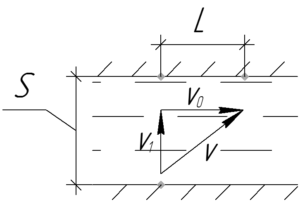Очевидно, что сколько времени катер переправлялся через реку, столько времени его и сносило течением. Так как катер двигался перпендикулярно течению в СО реки, то он попадет на другой берег за время:
\[S = {\upsilon _1}t \Rightarrow t = \frac{S}{{{\upsilon _1}}}\]
За это же время река перенесет катер вниз по течению на расстояние \(L\):
\[L = {\upsilon _0}t\]
Значит:
\[L = S\frac{{{\upsilon _0}}}{{{\upsilon _1}}}\]
Подсчитаем ответ:
\[L = 600\frac{{1,5}}{4} = 225\; м\]
Ответ: 225 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.12 Катер проходит расстояние между двумя пунктами на реке в обе стороны за 14 ч
1.7.14 Когда нет ветра, капли дождя оставляют на окне равномерно движущегося вагона
1.7.15 Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки
V_1 — это относительная скорость или абсолютная?
Скорость лодки на воде без течения v_1 = 5 м / с. Вода течет параллельно берегу со скоростью v_2 = 3 м / с. Как направить лодку, чтобы она пересекала реку в направлении, перпендикулярном берегу (какой должен быть угол между лодкой и берегом)? Сколько времени потребуется, чтобы лодка переправилась через реку шириной 80 метров?
в направлении перпендикулярном берегу означает просто угол 90 градусов или его нужно найти через арккосинус?
Лодку нужно направить под углом \(\alpha\) перпендикулярно реке в направлении противоположной течению, который можно найти так:\[\alpha = \arcsin \left( {\frac{{{\upsilon _2}}}{{{\upsilon _1}}}} \right)\]\[\alpha = \arcsin \left( {\frac{3}{5}} \right) = 36,9^\circ \]При этом скорость лодки относительно Земли можно найти по формуле:\[\upsilon = \sqrt {\upsilon _1^2 — \upsilon _2^2} \]\[\upsilon = \sqrt {{5^2} — {3^2}} = 4\;м/с\]Необходимое время равно:\[t = \frac{S}{\upsilon } = \frac{{80}}{4} = 20\;с\]
в условии ошибка
написано что катер двигался перпендикулярно течению но это не так
Имелось ввиду, что направление собственной скорости катера было перпендикулярно, но у нас есть еще течение реки, которое относит катер.
Катер двигался перпендикулярно течению реки — это означает, что скорость катера перпендикулярна скорости течения реки, не более того. Ошибки я не вижу.
очень понятно, объяснили доходчиво. спасибо большое!!!