icodepro.ruУсловие задачи:
Акула и подводная лодка начали двигаться одновременно из одной точки в одном направлении, лодка равномерно со скоростью 18 км/ч, а акула равноускоренно с ускорением 0,2 м/с2. На каком расстоянии друг от друга они будут находиться через 0,5 мин?
Задача №1.7.10 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=18\) км/ч, \(a_2=0,2\) м/с2, \(t=0,5\) мин, \(S-?\)
Решение задачи:
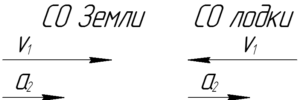Если в задаче описывается движение двух тел, и необходимо узнать как далеко они будут находиться друг от друга через некоторое время, то проще всего это сделать, перейдя в систему отсчета одного из тел. Давайте перейдем в систему отсчета (СО) лодки. В этой СО у акулы будет иметься вектор начальной скорости, равный \(– \overrightarrow {{\upsilon _1}}\). Это обусловлено тем, что при переходе в СО первого тела, нужно к векторам скорости и ускорения второго тела прибавить “минус” вектор скорости и вектор ускорения первого тела соответственно.
Тогда уравнение движения акулы в системе отсчета лодки выглядит так:
\[S = – {\upsilon _1}t + \frac{{{a_2}{t^2}}}{2}\]
Переведем некоторые исходные данные в систему СИ.
\[18\; км/ч = \frac{{18 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{180}}{{36}}\; м/с = 5\; м/с\]
\[0,5\; мин = 0,5 \cdot 60\; с = 30\; с\]
В итоге искомое расстояние \(S\) равно:
\[S = – 5 \cdot 30 + \frac{{0,2 \cdot {{30}^2}}}{2} = – 60\; м = -0,06\; км\]
Знак “минус” говорит о том, что акула не догонит лодку.
Ответ: 0,06 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.9 Автомобиль, двигаясь равномерно со скоростью 45 км/ч, в течение 10 с прошел
1.7.11 В течение какого времени скорый поезд длиной 280 м, следуя со скоростью
1.7.12 Катер проходит расстояние между двумя пунктами на реке в обе стороны за 14 ч
