icodepro.ruУсловие задачи:
Бомбардировщик пикирует на цель под углом 60° к горизонту со скоростью 540 км/ч и сбрасывает бомбу на высоте 600 м. На каком расстоянии от цели по горизонтальному направлению надо освободить бомбу, чтобы она попала в цель?
Задача №1.6.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(v_0=540\) км/ч, \(h=600\) м, \(L-?\)
Решение задачи:
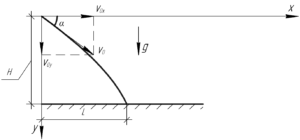Должно быть понятно, что бомба отличается от ракеты тем, что у нее нет двигателей, поэтому место попадания бомбы полностью определяется характеристиками движения бомбардировщика. В тот момент времени. когда бомбардировщик сбросит бомбу, она будет иметь тот же вектор скорости, что и самолет. Исходя из этого, приведем рисунок к этой задаче.
Запишем уравнения движения бомбы в проекциях на оси \(x\) и \(y\).
\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t + \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]
Обратите внимание во втором уравнении на знак “плюс”, он имеет место, поскольку \(v_у\) и \(g\) сонаправлены.
Найдем сколько времени будет падать бомба, для этого воспользуемся уравнением (2) и решим квадратное уравнение:
\[h = {v_0}\sin \alpha \cdot t + \frac{{g{t^2}}}{2}\]
\[g{t^2} + 2{v_0}\sin \alpha \cdot t – 2h = 0\]
\[D = 4v_0^2{\sin ^2}\alpha + 8gh\]
\[t = \frac{{ – 2{v_0}\sin \alpha \pm \sqrt {4v_0^2{{\sin }^2}\alpha + 8gh} }}{{2g}}\]
Заведомо видно, что один из корней получается отрицательным, остается следующий корень:
\[t = \frac{{ – 2{v_0}\sin \alpha + \sqrt {4v_0^2{{\sin }^2}\alpha + 8gh} }}{{2g}}\]
Подсчитаем время, поставив все известные величины в системе СИ. Покажем как перевести 540 км/ч в м/с.
\[540 \frac{км}{ч} = 540\frac{{1000}}{{3600}}\frac{м}{с} = 150\frac{м}{с}\]
\[t = \frac{{ – 2 \cdot 150 \cdot \sin 60^\circ + \sqrt {4 \cdot {{150}^2} \cdot {{\sin }^2}60^\circ + 8 \cdot 10 \cdot 600} }}{{2 \cdot 10}} = 4,0\; с.\]
Подставим полученное время в уравнение (1) и найдем ответ:
\[L = {v_0}\cos \alpha \cdot t\]
\[L = 150 \cdot \cos 60^\circ \cdot 4 = 300\; м.\]
Ответ: 300 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Смотрите также задачи:
1.6.12 Тело брошено с начальной скоростью 40 м/с под углом 30 градусов
1.6.14 Игрок посылает мяч с высоты 1,2 м над землей так, что угол
1.6.15 Камень, брошенный под углом к горизонту, упал на землю
Скажите, я направил ось y вверх, ось х как у вас, у меня получается : – V0sina t – gt^2/2 равное высоте, но выражая время оно получается отрицательно. Скажите почему так? Вроде правильно направил, проекция скорости по оси у направлена против самой оси как и ускорение свободного падения
У меня аналогичный вопрос , помогите)
Если начало координат Вы выбрали на уровне Земли, то уравнение движения в проекции на ось \(x\) должно выглядеть так:\[y = h – {\upsilon _0}\sin \alpha t – \frac{{g{t^2}}}{2}\]В момент попадания в цель \(y=0\), поэтому:\[0 = h – {\upsilon _0}\sin \alpha t – \frac{{g{t^2}}}{2}\]\[h = {\upsilon _0}\sin \alpha t + \frac{{g{t^2}}}{2}\]Получили точно такое же уравнение, как и в решении выше
Скажите а почему мы добавляем в выражение высоту? , мы же её ищем уравнением движения . Спасибо вам что помогаете , мне вас посоветовал преподаватель , теперь не могу оторваться от сайта , решаю постоянно.
Высота же дана в условии.
В уравнениях движения Вы обязательно должны учесть начальное положение тела относительно выбранной системы координат.
Для разных систем координат оно будет разным.
В решении задачи, представленной на этой странице, начальные координаты тела относительно выбранной системы координат равны \(x=0\) и \(y=0\), то есть (0;0). И если я подставлю время \(t=0\) в оба уравнения движения, то я получу \(x=0\) и \(y=0\). Значит уравнения движения (хотя бы в части начальных координат точек) записаны верно.
Если же ввести систему координат так, как сделали это Вы (ось \(x\) направлена как у меня, начало координат находится под точкой сброса бомбы на уровне Земли, и ось \(y\) направлена наверх), то начальные координаты тела относительно выбранной системы координат равны \(x=0\) и \(y=h\), то есть (0;h). Если я подставлю время \(t=0\) в уравнение движения (которое я привел в ответе на Ваш вопрос), то я получу \(y=h\) (уравнение движения по оси \(x\) у нас аналогичное).
И ещё почему в момент попадания y=0?
На своем рисунке из точки попадания в цель опустите перпендикуляр на ось \(y\) – он попадет в точку \(y=0\).
Если не ошибаюсь, но ведь Vy сонаправлен с g, а не Vx.
Точно, исправил опечатку, спасибо!
А разве бомба после отпускания не будет иметь ещё горизонтальной скорости?
Конечно. В момент отпускания бомба имеет такую же скорость, что и бомбардировщик. Учитывая, что бомбардировщик пикирует под углом \(\alpha\) к горизонту, то бомба в момент отпускания будет иметь скорость, равную по модулю \(\upsilon_0\). В проекции на ось \(x\) скорость бомбы равна \({\upsilon _0}\cos \alpha \), В проекции на ось \(y\) – \({\upsilon _0}\sin \alpha \), Вы это могли видеть по уравнениям движения бомбы в проекциях на оси координат.