icodepro.ruУсловие задачи:
Два поезда идут навстречу друг другу со скоростями 36 и 54 км/ч. Пассажир в первом поезде замечает, что второй поезд проходит мимо него в течение 6 с. Какова длина второго поезда?
Задача №1.7.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=36\) км/ч, \(\upsilon_2=54\) км/ч, \(t=6\) с, \(L_2-?\)
Решение задачи:
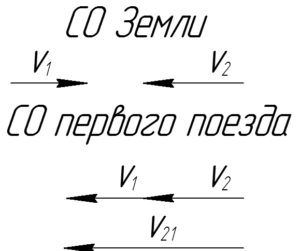Т.к. это пассажир видел, что второй поезд прошел мимо него за время \(t\), то чтобы взглянуть на событие от его лица, необходимо перейти в систему отсчета, связанную с пассажиром или с первым поездом, что одно и то же. Тогда вектор скорости второго поезда в системе отсчета первого \(\overrightarrow {{\upsilon _{21}}}\) можно найти, сложив вектор скорости второго поезда \(\overrightarrow {{\upsilon _2}} \) и вектор, равный по величине, но противоположный по направлению вектору первого поезда \( – \overrightarrow {{\upsilon _1}}\) (смотри рисунок).
Модуль вектора \(\overrightarrow {{\upsilon _{21}}}\) равен:
\[{\upsilon _{21}} = {\upsilon _1} + {\upsilon _2}\]
Находясь в СО первого поезда (он мысленно не движется) длину второго \(L_2\) определить очень просто из такой формулы:
\[{L_2} = {\upsilon _{21}}t\]
\[{L_2} = \left( {{\upsilon _1} + {\upsilon _2}} \right)t\]
Переведем исходные данные в систему СИ.
\[36\; км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{360}}{{36}}\; м/с = 10\; м/с \]
\[54\; км/ч = \frac{{54 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{540}}{{36}}\; м/с = 15\; м/с \]
В итоге численный ответ равен:
\[{L_2} = \left( {10 + 15} \right) \cdot 6 = 150\; м = 0,15\; км\]
Ответ: 0,15 км.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.7 Танк движется со скоростью 20 км/ч. С какими скоростями относительно дороги
1.7.9 Автомобиль, двигаясь равномерно со скоростью 45 км/ч, в течение 10 с прошел
1.7.10 Акула и подводная лодка начали двигаться одновременно из одной точки
решение не верно т.к 150м – это длина двух поездов: второй поезд также имеет длину, а это значит, что время за которое прошел второй поезд мимо первого начинается с первого вагона второго поезда и заканчивается выходом его последнего вагона:
начало отсчета:
<======1======!
<======2=====!
конец отсчета:
<======1======!
<====2====!
отступы не отображаются, но думаю и так все понято
Второй поезд едет время \(t\) мимо пассажира, а не мимо первого поезда, поэтому решение все же верное
3600 в знаменателе это что?
Это количество секунд в одном часе: 1 ч = 3600 с
Думаю что вы нашли длину первого поезда ,потому что второй поезд проходит за 6 с
со скоростью v1+v2 длину первого поезда
Нет, за 6 с мимо неподвижного пассажира со скоростью \(\upsilon_1 + \upsilon_2\) проходит второй поезд, поэтому мы нашли длину второго поезда
как тут +, если \({\upsilon _1}\) противоположен \({\upsilon _2}\), не понял
В решение написано, почему так: это из-за перехода в систему отсчета первого поезда. Относительная скорость второго поезда равна сумме скоростей поездов.
Могу привести жизненный пример: Вы едите на машине со скоростью 100 км/ч, по встречной полосе другая машина также со скоростью 100 км/ч. Очевидно, что относительно Вас другая машина едет со скоростью 200 км/ч. А вот если бы по Вашей полосе ехала машина со скоростью 100 км/ч, то её относительная скорость была бы равна 0, то есть она относительно Вас не двигалась бы.
А разве не V2=V1+V12 (скорость тела в неподвижной системе отсчёта равна векторной сумме его скорости относительно движущейся системы и скорости движущейся системы относительно неподвижной)
Это верно
Неужели нельзя вот так. 54+36=90:3.6=25 м/с*6 сек=150 метров. или ужели льзя
Вы решаете таким же образом