Условие задачи:
К концу первой секунды равнозамедленного движения модуль скорости тела равен 2 м/с, а к концу второй — 1 м/с. Определить модуль начальной скорости тела.
Задача №1.3.33 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=2\) м/с, \(\upsilon_2=1\) м/с, \(t_1=t_2=1\) с, \(\upsilon_0-?\)
Решение задачи:
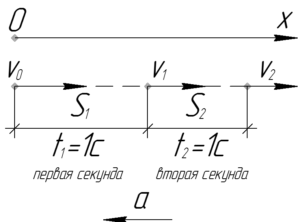 Из условия задачи следует, что скорость тела за одну \(t_2\) (вторую) секунду уменьшилась с 2 м/с до 1 м/с. Это дает нам возможность определить модуль ускорения тела согласно формуле-определению:
Из условия задачи следует, что скорость тела за одну \(t_2\) (вторую) секунду уменьшилась с 2 м/с до 1 м/с. Это дает нам возможность определить модуль ускорения тела согласно формуле-определению:
\[a = \frac{{\left| {{\upsilon _2} — {\upsilon _1}} \right|}}{t_2}\]
Зная, что \({\upsilon _2} < {\upsilon _1}\), раскроем модуль в числителе.
\[a = \frac{{{\upsilon _1} — {\upsilon _2}}}{t_2}\]
Если нам нужно узнать начальную скорость \(\upsilon_0\), то запишем формулу скорости для равнозамедленного движения:
\[\upsilon = {\upsilon _0} — at\]
Так как через одну \(t_1\) секунду после начала движения скорость тела стала равной \(\upsilon_1\), запишем:
\[{\upsilon _1} = {\upsilon _0} — at_1\]
\[{\upsilon _0} = {\upsilon _1} + at_1\]
Подставим выражение для ускорения \(a\) и получим конечную формулу.
\[{\upsilon _0} = {\upsilon _1} + \frac{{{\upsilon _1} — {\upsilon _2}}}{t_2}t_1\]
Так как \(t_1=t_2\), то:
\[{\upsilon _0} = 2{\upsilon _1} — {\upsilon _2}\]
\[{\upsilon _0} = 2 \cdot 2 — 1 = 3\; м/с \]
Ответ: 3 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.32 За седьмую секунду равноускоренного движения модуль вектора скорости
1.3.34 На некотором отрезке пути скорость тела увеличилась с 12 см/с до 16 см/с
1.3.35 Ракета летит со скоростью 4 км/с. Затем она движется с постоянным ускорением

 icodepro.ru
icodepro.ru
А если найти ускорение через формулу Vк=Vн-аt, то есть 1=2-а, то есть ускорение равно 3. А потом через эту же формулу найти начальную скорость 2=V0 — 3. И получается 5 мс. Что не так?
У Вас ускорение должно получиться 1 м/с2, а не 3 м/с2, Вы неправильно решаете свое уравнение \(1 = 2 — a\).