Условие задачи:
Какова линейная скорость точек на ободе колеса паровой турбины с диаметром колеса 1 м и частотой вращения 300 об/мин?
Задача №1.8.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(D=1\) м, \(\nu=300\) об/мин, \(\upsilon-?\)
Решение задачи:
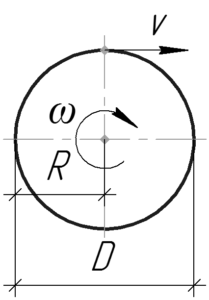 Линейную скорость точек \(\upsilon\) на ободе легко определить, зная угловую скорость \(\omega\) и радиус колеса \(R\). Так как радиус равен половине диаметра, то:
Линейную скорость точек \(\upsilon\) на ободе легко определить, зная угловую скорость \(\omega\) и радиус колеса \(R\). Так как радиус равен половине диаметра, то:
\[\upsilon = \omega R = \frac{{\omega D}}{2}\]
Теперь необходимо определить угловую скорость \(\omega\). Это можно сделать по формуле связи угловой скорости \(\omega\) и частоты вращения \(\nu\):
\[\omega = 2\pi \nu \]
Подставим её в первую формулу, тогда получим ответ в общем виде.
\[\upsilon = \frac{{2\pi \nu D}}{2} = \pi \nu D\]
Подставляя численные значения в формулу, необходимо не забывать, что их нужно переводить в систему СИ.
\[300\; [1/мин] = \frac{{300}}{{60}}\; [1/с] = 5\; [1/с]\]
Единицу измерения 1/с называют Гц (Герц).
Также хочется отметить, что в физике нет такого понятия как «обороты», поэтому правильнее не 300 об/мин, а 300 1/мин. Обороты, количество молекул и т.д. в физике считаются безразмерными.
Считаем ответ:
\[\upsilon = 3,14 \cdot 5 \cdot 1 = 15,7\; м/с = 942\; м/мин\]
Ответ: 942 м/мин.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.27 При движении моторной лодки по течению реки ее скорость относительно берега
1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.3 Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает

 icodepro.ru
icodepro.ru