Камень, брошенный под углом к горизонту, упал на землю

Условие задачи:

Камень, брошенный под углом к горизонту, упал на землю со скоростью 10 м/с. Чему равна высота подъема камня, если известно, что во время движения его максимальная скорость была вдвое больше минимальной?

Задача №1.6.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(v=10\) м/с, \(v_{max}=2v_{min}\), \(H-?\)

Решение задачи:

Стоит заметить, что с какой скоростью тело упало на землю – с такой же скоростью оно было и брошено, то есть:

\[{\upsilon _0} = \upsilon \]

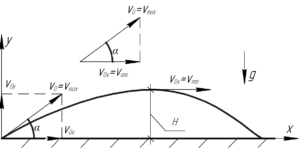На сайте уже разбиралась задача, в которой поднимался вопрос о том, где тело, брошенное под углом к горизонту, будет иметь минимальную и максимальную скорость. Напомним, что первая имеет место быть в наивысшей точке подъема, а вторая – в момент бросания и падения. Представим рисунок, для лучшего понимания решения задачи.

Из треугольника, изображенного на рисунке сверху, справедливо:

\[\cos \alpha  = \frac{{{v_{\min }}}}{{{v_{\max }}}}\]

\[\cos \alpha  = \frac{{{v_{\min }}}}{{2{v_{\min }}}} = \frac{1}{2} \Rightarrow \alpha  = 60^\circ \]

Запишем уравнения движения и уравнения скорости в проекции на оси \(x\) и \(y\):

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,\,(2) \hfill \\
\end{gathered} \right.\]

\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt\,\,(4) \hfill \\
\end{gathered} \right.\]

В наивысшей точке подъема вертикальная составляющая скорости равна нулю, поэтому из уравнения (4) найдем время подъема и, подставив его в уравнение (2), получим выражение для определения максимальной высоты подъема.

\[{v_y} = 0 \Rightarrow {v_0}\sin \alpha  – gt = 0\]

\[t = \frac{{{v_0}\sin \alpha }}{g}\]

\[H = {v_0}\sin \alpha  \cdot t – \frac{{g{t^2}}}{2}\]

\[H = {v_0}\sin \alpha  \cdot \frac{{{v_0}\sin \alpha }}{g} – \frac{g}{2} \cdot \frac{{v_0^2{{\sin }^2}\alpha }}{{{g^2}}}\]

\[H = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\]

Осталось подставить в выведенную формулу исходные данные и полученный нами угол \(\alpha  = 60^\circ\).

\[H = \frac{{10^2 \cdot {{\sin }^2}60^\circ }}{{2 \cdot 10}} = 3,75\; м.\]

Ответ: 3,75 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.6.14 Игрок посылает мяч с высоты 1,2 м над землей так, что угол
1.6.16 Из орудия сделан выстрел вверх по склону горы. Угол наклона горы
1.6.17 Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода