Камень, брошенный с земли под углом 45 градусов к горизонту

Условие задачи:

Камень, брошенный с земли под углом 45° к горизонту, через 0,8 с после начала движения имел вертикальную составляющую скорости 12 м/с. Чему равно расстояние между точкой бросания и местом падения камня?

Задача №1.6.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=45^\circ\), \(t_1=0,8\) с, \(v_y=12\) м/с, \(L-?\)

Решение задачи:

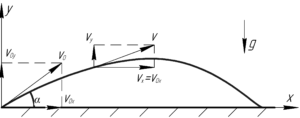Для решения задачи необходимо сделать рисунок. Мы его сделали за вас, можете взглянуть на него справа, для увеличения кликнув на нем мышью.

Поскольку нужно определить дальность полета, то запишем уравнения движения камня в проекциях на введенные нами оси, а далее уже определим, каких данных нам не хватает. Уравнения, как всегда, выглядят стандартно, поскольку в задаче нет ничего необычного.

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,(2) \hfill \\
\end{gathered} \right.\]

Когда камень ударится о землю, его ордината \(y\) будет равна нулю, поэтому приравняем уравнение (2) к нулю и найдем корни получившегося уравнения.

\[y = 0 \Rightarrow {v_0}\sin \alpha  \cdot t – \frac{{g{t^2}}}{2} = 0\]

\[t\left( {{v_0}\sin \alpha – \frac{{gt}}{2}} \right) = 0\]

\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{v_0}\sin \alpha }}{g} \hfill \\
\end{gathered} \right.\]

Первый корень не удовлетворяет условию падения камня, поскольку он не мог взлететь и удариться о землю в ту же секунду.

Тогда второй корень подставим в уравнение (1) и получим формулу для определения дальности полета.

\[L = \frac{{2{v_0}\cos \alpha  \cdot {v_0}\sin \alpha }}{g} = \frac{{v_0^2\sin 2\alpha }}{g}\]

Отлично, значит нам необходимо узнать начальную скорость камня (в момент броска), и после мы сможем сосчитать ответ. Для этого запишем уравнение скорости для вертикальной ее составляющей.

\[{v_y} = {v_{0y}} – gt_1 = {v_0}\sin \alpha  – gt_1\]

Из него выразим начальную скорость камня и подставим ее в формулу дальности полета.

\[{v_0} = \frac{{{v_y} + gt_1}}{{\sin \alpha }}\]

В итоге получена формула в общем виде:

\[L = {\left( {\frac{{{v_y} + gt_1}}{{\sin \alpha }}} \right)^2}\frac{{\sin 2\alpha }}{g}\]

Как всегда, подставим все известные величины в СИ и подсчитаем ответ:

\[L = {\left( {\frac{{12 + 10 \cdot 0,8}}{{\sin 45^\circ }}} \right)^2}\frac{{\sin 90^\circ }}{{10}} = 80\; м\]

Ответ: 80 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.2 Баскетболист бросает мяч в кольцо. Скорость мяча после броска
1.6.4 Минимальная скорость при движении тела, брошенного под углом
1.6.5 На некоторой высоте одновременно из одной точки брошены