Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после

Условие задачи:

Катер, плывущий вниз по реке, догоняет спасательный круг. Через 30 мин после встречи с кругом катер поворачивает назад и снова встречает круг на расстоянии 5 км от места первой встречи. Определите скорость течения реки. Мощность катера постоянна.

Задача №1.7.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(t=30\) мин, \(S=5\) км, \(\upsilon_т-?\)

Решение задачи:

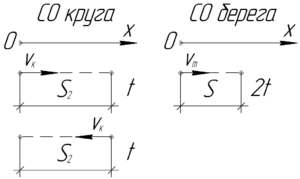Для начала нужно понять такой факт – в системе отсчета (СО) круга (или реки, что одно и то же) скорость катера не зависит от направления движения (по течению или против течения). Учитывая это, рассмотрим движение катера в этой СО после первой встречи со спасательным кругом. Он “убегал” от круга в течение времени \(t\) со скоростью \(\upsilon_к\) и допустим прошел путь \(S_2\). Но ведь когда он развернется, то до круга он будет плыть то же расстояние \(S_2\) (замечу, что только в СО круга) и с такой же скоростью \(\upsilon_к\), а значит затратит на это то же время \(t\). Значит между первой и второй встречей прошло время, равное \(2t\).

Теперь вернемся к СО, связанной с берегом. Круг плывет равномерно со скоростью течения \(\upsilon_т\) и за время, равное (как мы уже определили) \(2t\), пройдет расстояние \(S\). Будет правильно записать:

\[S = {\upsilon _т} \cdot 2t \Rightarrow {\upsilon _т} = \frac{S}{{2t}}\]

Напомню, что 30 мин – это 0,5 часа.

\[{\upsilon _1} = \frac{5}{{2 \cdot 0,5}} = 5\; км/ч =1,4\; м/с\]

Ответ: 1,4 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.7.22 Кран равномерно поднимает груз со скоростью 0,3 м/с и одновременно движется
1.7.24 Автомобиль движется со скоростью 12 м/с. Чему равен модуль линейной скорости верхней
1.7.25 Человек бежит со скоростью 5 м/с относительно палубы теплохода в направлении