Условие задачи:
Когда нет ветра, капли дождя оставляют на окне равномерно движущегося вагона линии, направленные под углом 60° к вертикали. Какова скорость капель относительно Земли, если поезд движется со скоростью 72 км/ч?
Задача №1.7.14 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(\upsilon_0=72\) км/ч, \(\upsilon_1-?\)
Решение задачи:
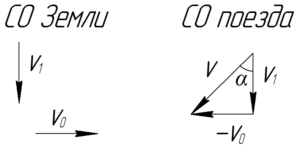 В системе отсчета (СО) Земли капля падает вниз, а поезд, допустим, едет вправо. Перейдем в СО поезда. Для этого к вектору скорости капли \(\overrightarrow {{\upsilon _1}}\) прибавим вектор, равный по величине и противоположный по направлению вектору скорости поезда, то есть \( — \overrightarrow {{\upsilon _0}}\). В итоге имеем вектор \(\overrightarrow \upsilon\), направление которого совпадает с направлением линий, которые оставляют капли на окне движущегося вагона.
В системе отсчета (СО) Земли капля падает вниз, а поезд, допустим, едет вправо. Перейдем в СО поезда. Для этого к вектору скорости капли \(\overrightarrow {{\upsilon _1}}\) прибавим вектор, равный по величине и противоположный по направлению вектору скорости поезда, то есть \( — \overrightarrow {{\upsilon _0}}\). В итоге имеем вектор \(\overrightarrow \upsilon\), направление которого совпадает с направлением линий, которые оставляют капли на окне движущегося вагона.
Теперь смотрим на рисунок. Зная, что изображен прямоугольный треугольник, легко найти искомую скорость \(\upsilon_1\):
\[\frac{{{\upsilon _0}}}{{{\upsilon _1}}} = tg\alpha \Rightarrow {\upsilon _1} = \frac{{{\upsilon _0}}}{{tg\alpha }}\]
Вычислим ответ, подставим исходные данные задачи.
\[{\upsilon _1} = \frac{{72}}{{tg60^\circ }} = 41,57\; км/ч\]
Ответ: 41,57 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.7.13 Катер, переправляясь через реку шириной 600 м, двигался перпендикулярно
1.7.15 Моторная лодка проходит расстояние между двумя пунктами A и B по течению реки
1.7.16 Пассажир едет в поезде, скорость которого 80 км/ч. Навстречу этому поезду

 icodepro.ru
icodepro.ru
а где здесь

абсолютная скорость,
относительная скорость,
переносная скорость?
Автор сайта вроде бы неплохо решает задачи по физике, но, с точки русского языка, наблюдается полное косноязычие и излишнее словоблудие!