icodepro.ruУсловие задачи:
Маховое колесо вращается с угловой скоростью 10 рад/с. Модуль линейной скорости некоторой точки маховика равен 2 м/с. Каков модуль линейной скорости точки, находящейся дальше от оси маховика на 0,1 м?
Задача №1.8.34 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\omega=10\) рад/с, \(\upsilon_1=2\) м/с, \(\Delta R=0,1\) м, \(\upsilon_2-?\)
Решение задачи:
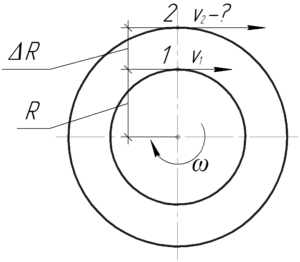Обе точки вращаются с одной и той же угловой скоростью \(\omega\), но находятся на разных расстояниях от оси вращения: первая – на расстоянии \(R\), вторая – на расстоянии \(\left( {R + \Delta R} \right)\), из-за этого они имеют разные линейные скорости. Запишем такую систему:
\[\left\{ \begin{gathered}
{\upsilon _1} = \omega R \;\;\;\;(1)\hfill \\
{\upsilon _2} = \omega \left( {R + \Delta R} \right) \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Вычтем из выражения (2) выражение (1).
\[{\upsilon _2} – {\upsilon _1} = \omega \Delta R\]
\[{\upsilon _2} = {\upsilon _1} + \omega \Delta R\]
Остается только посчитать ответ.
\[{\upsilon _2} = 2 + 10 \cdot 0,1 = 3\; м/с\]
Ответ: 3 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.33 Линейная скорость точки на ободе равномерно вращающегося колеса диаметром
1.8.35 Колесо имеет угловую скорость вращения 2pi рад/с. За какое время оно делает
1.8.36 У паровой турбины радиус рабочего колеса в 8 раз меньше, а число оборотов
