Условие задачи:

Материальная точка движется по окружности. Угол поворота радиуса, соединяющего материальную точку с центром окружности, изменяется по закону $\varphi=5t$ рад. Определите центростремительное ускорение через 4 с, если радиус окружности равен 0,05 м.

Задача №1.8.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\varphi=5t$, $t=4$ с, $R=0,05$ м, $a_ц-?$

Решение задачи:

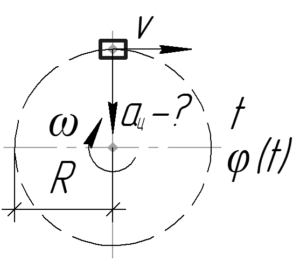Так как в условии дан закон изменения угла поворота, то логичным бы было записать формулу определения центростремительного ускорения через какую-то угловую характеристику, например, угловую скорость.

$$a_ц = {\omega ^2}R$$

При равномерном движении по окружности общее уравнение изменения угла поворота выглядит так:

$$\varphi  = \omega t$$

Сопоставляя с данным уравнением $\varphi=5t$, можно сделать вывод, что угловая скорость равна 5 рад/с.

$$\omega  = 5\; рад/с$$

Вы получили бы тот же самый результат, если взяли производную от $\varphi \left( t \right)$, так как функция изменения угловой скорости $\omega \left( t \right)$ есть первая производная от функции изменения угла поворота $\varphi’ \left( t \right)$.

$$\omega \left( t \right) = \varphi’ \left( t \right)$$

В конечном итоге центростремительное ускорение равно:

$$a_ц = {5^2} \cdot 0,05 = 1,25\; м/с^2$$

Ответ: 1,25 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.8.18 Вычислить путь, который проехал за 30 с велосипедист, двигающийся с угловой
1.8.20 Найти радиус вращающегося колеса, если линейная скорость точки на ободе
1.8.21 Обруч катится по горизонтальной плоскости без проскальзывания со скоростью

Милые путаны встречаются с обеспеченным мужчинами для приятного отдыха, лучшие феи проститутки Набережные Челны, доставят тебе незабываемое ощущение. Среди анкет этого интернет - ресурса oopschelny.ru, вы сможете найти для себя проститутку на час или на ночь. Позитивные лучшие феи проститутки Набережные Челны, желанные и восхитительные, они такие изобретательные и стройные, что тебе обязательно захочется секса. Не упусти свой шанс.