Минимальная скорость при движении тела, брошенного под углом

Условие задачи:

Минимальная скорость при движении тела, брошенного под углом к горизонту, равна 5 м/с, а максимальная 10 м/с. Определить угол, под которым брошено тело.

Задача №1.6.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(v_{min}=5\) м/с, \(v_{max}=10\) м/с, \(\alpha-?\)

Решение задачи:

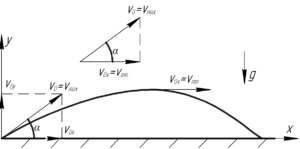Сделаем изображение к задаче, смотрите его справа.

Для объяснения решения я буду использовать следующий факт, что в любой момент времени скорость тела можно разложить на составляющие, тогда самую разлагаемую скорость можно найти по теореме Пифагора:

\[v = \sqrt {v_x^2 + v_y^2} \]

Теперь вспомним тот факт, что при движении тела, брошенного под углом к горизонту, горизонтальная составляющая скорости \(v_x\) не изменяется, поскольку движение вдоль \(x\) является равномерным (вдоль этой оси не действуют силы), а вертикальная составляющая скорости \(v_y\) меняется от максимального в момент бросания до нуля в наивысшей точке, и обратно. Причем в момент падения на землю обе составляющие (а значит и сама скорость) будут такими же, как при бросании (если, конечно же, принимать поверхность земли плоской, как у нас на рисунке).

Получается, что если скорость определяется приведенной выше формулой, то минимальное значение она примет в наивысшей точке, когда \(v_y=0\) м/с, а максимальное – в момент бросания и падения обратно на поверхность земли.

\[\left[ \begin{gathered}
{v_{\min }} = {v_x} = {v_{ox}} \hfill \\
{v_{\max }} = {v_0} \hfill \\
\end{gathered} \right.\]

Взглянув на рисунок, можно увидеть, что угол между векторами, соответствующими этим скоростям, и есть угол бросания тела. Для этого прямоугольного треугольника косинус угла \(\alpha\) определяется по следующей формуле.

\[\cos \alpha  = \frac{{{v_{0x}}}}{{{v_0}}},\cos \alpha  = \frac{{{v_{\min }}}}{{{v_{\max }}}} \Rightarrow \alpha  = \arccos \frac{{{v_{\min }}}}{{{v_{\max }}}}\]

Подставим известные данные и получим ответ:

\[\alpha  = \arccos \frac{5}{{10}} = 60^\circ \]

Ответ: 60°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.3 Камень, брошенный с земли под углом 45 градусов к горизонту
1.6.5 На некоторой высоте одновременно из одной точки брошены
1.6.6 Под каким углом к горизонту нужно бросить тело, чтобы высота