Решение: Мяч, брошенный под некоторым углом к горизонту с начальной

Условие задачи:

Мяч, брошенный под некоторым углом к горизонту с начальной скоростью 10 м/с, через 0,5 с имел скорость 7 м/с. Определите максимальную высоту подъема мяча и время всего движения.

Задача №1.6.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(v_0=10\) м/с, \(t=0,5\) с, \(v=7\) м/с, \(H-?\), \(\tau-?\)

Решение задачи:

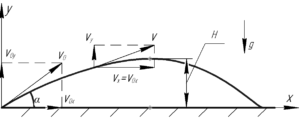Рисунок, поясняющий решение задачи, изображен справа, вы можете увеличить его для просмотра, кликнув на нем мышью.

Чтобы решить эту задачу, запишем уравнение скорости в проекциях на оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt\,\,\,(2) \hfill \\
\end{gathered} \right.\]

Полную скорость в любой момент времени можно найти по теореме Пифагора:

\[v = \sqrt {v_x^2 + v_y^2} \]

Подставим составляющие скорости в это уравнение:

\[v = \sqrt {v_0^2{{\cos }^2}\alpha + {{({v_0}\sin \alpha – gt)}^2}} \]

Раскроем квадрат под корнем и произведем некоторые тригонометрические преобразования:

\[v = \sqrt {v_0^2 – 2{v_0}\sin \alpha \cdot gt + {g^2}{t^2}} \]

Возведем обе части уравнения в квадрат и выразим \(\sin \alpha\):

\[{v^2} = v_0^2 – 2{v_0}\sin \alpha \cdot gt + {g^2}{t^2}\]

\[\sin \alpha = \frac{{v_0^2 + {g^2}{t^2} – {v^2}}}{{2{v_0}gt}}\]

Не будем тащить эту громоздкую формулу через всю задачу, чтобы решить ее в общем виде, поэтому я с вашего позволения подставлю исходные данные сейчас, чтобы сосчитать \(\sin \alpha\):

\[\sin \alpha = \frac{{{{10}^2} + {{10}^2} \cdot {{0,5}^2} – {7^2}}}{{2 \cdot 10 \cdot 10 \cdot 0,5}} = 0,76\]

Найдем время подъема, приравняв уравнение (2) к нулю, поскольку в наивысшей точке подъема вертикальная составляющая скорости равна нулю.

\[{v_y} = 0 \Rightarrow {v_0}\sin \alpha – g{t_1} = 0\]

\[{t_1} = \frac{{{v_0}\sin \alpha }}{g}\]

Кстати, полное время полета (а его нам нужно определить) равно удвоенному времени подъема.

\[\tau = 2{t_1} = \frac{{2{v_0}\sin \alpha }}{g}\]

\[\tau = \frac{{2 \cdot 10 \cdot 0,76}}{{10}} = 1,52\; с.\]

Для нахождения высоты подъема, необходимо подставить время подъема \(t_1\) в уравнение движения в проекции на ось \(y\), для чего их и запишем.

\[\left\{ \begin{gathered}
ox:\,\,x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\
oy:\,\,y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,(4) \hfill \\
\end{gathered} \right.\]

Получаем ответ в общем виде:

\[H = {v_0}\sin \alpha \cdot \frac{{{v_0}\sin \alpha }}{g} – \frac{g}{2}{\left( {\frac{{{v_0}\sin \alpha }}{g}} \right)^2} = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\]

Подставим все известные нам величины в СИ, будем иметь ответ и на второй вопрос задачи.

\[H = \frac{{{{10}^2} \cdot {{0,76}^2}}}{{2 \cdot 10}} = 2,89\; м.\]