Мяч, брошенный со скоростью 10 м/с под углом 45 градусов

Условие задачи:

Мяч, брошенный со скоростью 10 м/с под углом 45° градусов к горизонту, ударяется о вертикальную стенку, находящуюся на расстоянии 3 м от места бросания. Определить модуль скорости мяча после удара, если удар абсолютно упругий.

Задача №1.6.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(v_0=10\) м/с, \(\alpha=45^\circ\), \(L=3\) м, \(v-?\)

Решение задачи:

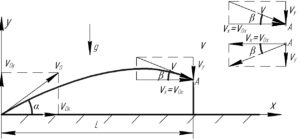Для более лучшего понимания решения задачи приведем к ней рисунок.  Как и во всех задачах на движение тела под углом к горизонту запишем уравнения движения тел в проекция на введенные нами оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:\,\,x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:\,\,y = {v_0}\sin \alpha \cdot t – \frac{{g{t^2}}}{2}\,\,(2) \hfill \\
\end{gathered} \right.\]

Хорошо, но условием дано расстояние до стенки, поэтому применим уравнение (1) и найдем сколько времени длился полета до удара о препятствие.

\[L = {v_0}\cos \alpha  \cdot t \Rightarrow t = \frac{L}{{{v_0}\cos \alpha }}\]

Поскольку удар абсолютно упругий, то скорость мяч до соударения равна скорости мяча после него (поскольку нет потерь кинетической энергии). Этот факт проиллюстрирован справа на нашем рисунке. Видно, что в момент удара горизонтальная составляющая скорости мяча меняет свое направление, а вертикальная – остается такой же. Поэтому нет разницы что определять: модуль скорости мяча после удара или до него.

Запишем теперь уравнения скорости в проекциях на оси координат:

\[\left\{ \begin{gathered}
ox:{v_x} = {v_0}\cos \alpha \,\,\,\,\,\,\,\,\,\,\,\,\,(3) \hfill \\
oy:{v_y} = {v_0}\sin \alpha – gt\,\,\,(4) \hfill \\
\end{gathered} \right.\]

Искомая нами скорость легко находится из теоремы Пифагора:

\[v = \sqrt {v_x^2 + v_y^2} \]

Подставим в эту формулу уравнения (3) и (4).

\[v = \sqrt {v_0^2{{\cos }^2}\alpha  + {{({v_0}\sin \alpha  – gt)}^2}} \]

Заменим в этой формуле неизвестное \(t\) на полученную нами формулу для его определения, в итоге имеем ответ в общем виде:

\[v = \sqrt {v_0^2{{\cos }^2}\alpha  + {{({v_0}\sin \alpha  – g\frac{L}{{{v_0}\cos \alpha }})}^2}} \]

Подставим в формулу исходные данные в системе измерения СИ и будем иметь численный ответ:

\[v = \sqrt {{{10}^2} \cdot {{\cos }^2}45^\circ  + {{(10 \cdot \sin 45^\circ  – 10\frac{3}{{10 \cdot \cos 45^\circ }})}^2}}  = 7,62\; м/с = 27,43\; км/ч\]

Ответ: 27,43 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.7 Мяч, брошенный под некоторым углом к горизонту с начальной
1.6.9 Пуля вылетает из ствола под углом 45 градусов к горизонту
1.6.10 Снаряд вылетает из орудия со скоростью 1000 м/с под углом 60