Условие задачи:

Мяч, брошенный вертикально вверх, упал на землю через 3 с. Чему равна величина скорости мяча в момент падения?

Задача №1.4.51 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$t=3$ с, $\upsilon_0-?$

Решение задачи:

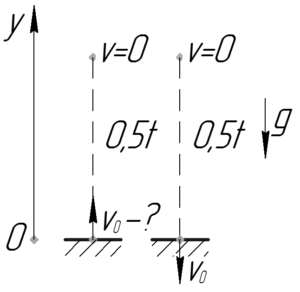Согласно закону сохранения энергии скорость мяча в момент падения равна скорости $\upsilon_0$, с которой изначально бросили мяч (поэтому на рисунке мы и начальную, и конечную скорость обозначили как $\upsilon_0$).

Если мяч, брошенный с земли, вернулся на землю через некоторое время $t$, то максимальной высоты он достиг через $\frac{t}{2}$ секунд.

Запишем уравнение скорости для тела, брошенного с земли вертикально вверх. В этом уравнении $t$ — это переменная скорости.

$$oy:\upsilon  = {\upsilon _0} — gt$$

В точке наивысшего подъема его скорость, очевидно, будет равна нулю. Там мяч окажется через $t=\frac{t}{2}$ секунд. Поэтому:

$$0 = {\upsilon _0} — g\frac{t}{2}$$

В конечном счете:

$${\upsilon _0} = g\frac{t}{2}$$

Подсчитаем ответ:

$${\upsilon _0} = 10\frac{3}{2} = 15\; м/с$$

Ответ: 15 м/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.50 За последнюю секунду свободно падающее без начальной скорости тело
1.5.1 Камень брошен горизонтально со скоростью 5 м/с. Через 0,8 с он упал
1.5.2 Камень брошен с некоторой высоты в горизонтальном направлении и упал

Встречаются реальные проститутки Челябинска индивидуально в апартаментах и на выезд - wowchel.ru. Задавайте тему для ролевых игр и будете приятно удивлены сноровкой и воображением проституток города. Лучшие в городе реальные проститутки Челябинска, страстные и желанные, они такие грациозные и неуёмные, что любой захочет их. Не упусти свой шанс.