Условие задачи:
Найти радиус вращающегося колеса, если линейная скорость точки на ободе в 3 раза больше линейной скорости точки, лежащей на 40 см ближе к оси колеса.
Задача №1.8.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_1=3\upsilon_2\), \(\Delta R=40\) см, \(R-?\)
Решение задачи:
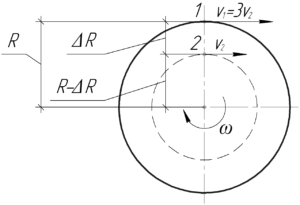 Запишем формулу линейной скорости \(\upsilon\) точки, находящейся на расстоянии \(R\) от оси и вращающейся с угловой скоростью \(\omega\).
Запишем формулу линейной скорости \(\upsilon\) точки, находящейся на расстоянии \(R\) от оси и вращающейся с угловой скоростью \(\omega\).
\[\upsilon = \omega R\]
Далее запишем в системе линейные скорости двух рассматриваемых точек, учитывая, что они вращаются с одинаковой угловой скоростью, но находятся на разных расстояниях от оси вращения.
\[\left\{ \begin{gathered}
{\upsilon _1} = \omega R \hfill \\
{\upsilon _2} = \omega \left( {R — \Delta R} \right) \hfill \\
\end{gathered} \right.\]
Поделим первое выражение системы на второе.
\[\frac{{{\upsilon _1}}}{{{\upsilon _2}}} = \frac{R}{{R — \Delta R}}\]
Так как по условию скорость точки 1 в 3 раза больше скорости точки 2, то:
\[\frac{{3{\upsilon _2}}}{{{\upsilon _2}}} = \frac{R}{{R — \Delta R}} \Rightarrow \frac{R}{{R — \Delta R}} = 3\]
\[R = 3R — 3\Delta R\]
\[2R = 3\Delta R\]
\[R = \frac{3}{2}\Delta R\]
Радиус колеса численно равен:
\[R = \frac{3}{2} \cdot 40 = 60\; см = 0,6\; м\]
Ответ: 0,6 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.19 Материальная точка движется по окружности. Угол поворота радиуса, соединяющего
1.8.21 Обруч катится по горизонтальной плоскости без проскальзывания со скоростью
1.8.22 Точки окружности вращающегося диска имеют линейную скорость по модулю

 icodepro.ru
icodepro.ru