icodepro.ruУсловие задачи:
Найти скорость движения автомобиля, если его колесо диаметром 1,1 м делает 309 оборотов в минуту.
Задача №1.8.3 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(D=1,1\) м, \(\nu=309\) об/мин, \(\upsilon-?\)
Решение задачи:
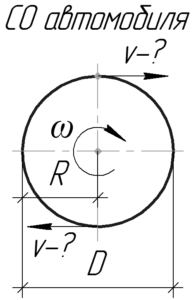Строго говоря, относительно Земли точки колеса при движении автомобиля совершают сложное движение, при котором они двигаются и поступательно, и вращательно. Но если перейти в систему отсчета (СО), связанную с автомобилем, то колеса будут уже совершать простое вращательное движение. При этом понятно, что линейная скорость крайних точек колеса равна скорости движения автомобиля \(\upsilon\).
Эту линейную скорость можно определить по такой формуле, учитывая, что радиус равен одной второй диаметра:
\[\upsilon = \omega R = \frac{{\omega D}}{2}\;\;\;\;(1)\]
Угловую скорость \(\omega\) найдем, используя частоту вращения \(\nu\), данную в условии, по такому выражению:
\[\omega = 2\pi \nu \;\;\;\;(2)\]
Подставим (2) в (1):
\[\upsilon = \frac{{2\pi \nu D}}{2} = \pi \nu D\]
Перед тем, как подставлять значения и вычислять ответ, переведем частоту вращения в систему СИ.
\[309\; [1/мин] = \frac{{309}}{{60}}\; [1/с] = \frac{{103}}{{20}}\; [1/с]\]
\[\upsilon = 3,14 \cdot \frac{{103}}{{20}} \cdot 1,1 = 17,79\; м/с\]
Ответ: 17,79 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.2 Какова угловая скорость вращения колеса, делающего 240 оборотов
1.8.4 С какой скоростью едет велосипедист, если колесо делает 100 об/мин. Радиус
1.8.5 Угол поворота колеса радиусом 0,2 м изменяется по закону phi=9,42t (рад)
объект вращается по окружности с периодом 1 минута. Найдите количество оборотов тела за 600 секунд.
Автомобиль движется с скоростью 36 км/ч.
Определите скорость верхней и нижней точки колеса относительно земли
Миша рассчитывает параметры движения колеса. Кoлeco paдиуcoм 40 cм дeлaeт oдин oбopoт зa 0,4 ceкунды. Haйди cкopocть тoчeк нa oбoдe кoлeca.
Ну совсем же просто…
Любая точка на ободе колеса за один оборот пройдет расстояние, равное:\[S = 2\pi R\]Если она проходит это расстояние за время, равное одному периоду \(T\), то её линейная скорость \(\upsilon\) равна:\[\upsilon = \frac{S}{T} = \frac{{2\pi R}}{T}\]Численный ответ:\[\upsilon = \frac{{2 \cdot 3,14 \cdot 0,4}}{{0,4}} = 6,28\;м/с\]
Автомобиль радиусом 0,5 м совершил 500 оборотов ,Какое расстояние проедет автомобиль?
Автомобиль радиусом?
Правильно же: автомобиль с колесами радиусом…
Простая же задача, почему не можете решить сами? Представьте, что Вы сели на велосипед и поехали. При этом колеса Вашего велосипеда сделали один оборот. Понятно, что Вы проедите расстояние равное длине окружности колес Вашего велосипеда, т.е. \({S_0} = 2\pi R\). А если колеса сделают \(N\) оборотов? Тогда Вы проедите в \(N\) раз большее расстояние, т.е. \(S = N \cdot 2\pi R\). Ваша задача абсолютна аналогична, поэтому:\[S = N \cdot 2\pi R\]\[S = 500 \cdot 2 \cdot 3,14 \cdot 0,5 = 1570\;м\]
Интуитивно понятно,что скорость вращения колеса и автомобиля идентичны,но как строго доказать?
Если Вы смотрите на колесо автомобиля, находясь в нем (т.е. в системе отсчета (СО), связанной с автомобилем), то Вы видите, что все точки на краю колеса вращаются вокруг оси с одинаковой линейной скоростью \(\upsilon\) (колесо для Вас совершает обыкновенное вращательное движение).
Далее нужно понять, что колесо обычно не проскальзывает (в задаче как раз этот случай). Это значит, что скорость точки земли (для Вас в СО автомобиля), соприкасающейся с колесом также равна \(\upsilon\) (т.е. относительная скорость этих двух точек равна нулю).
В итоге, если для Вас в СО автомобиля земля уходит, например, назад со скоростью \(\upsilon\), значит в СО земли автомобиль едет вперед со скоростью \(\upsilon\).
Можно доказать еще более строго, но тогда нужно вводить понятие плоскопараллельного движения, а это выходит за рамки школьного курса физики…
Где будет находится Максимальное значение модуля вектора скорости материальной точки на ободе колеса?
В самой верхней точке колеса
При номинальной скорости вращения якоря 3000 об/мин машина развивает на зажимах напряжение 24 В .как найти скорость вращения двигателя когда вольтметр показывает 16 в ?помогите пожалуйста мозгов не хватает …
Напряжение пропорционально скорости вращения якоря, поэтому:\[\frac{{{U_1}}}{{{U_2}}} = \frac{{{\nu _1}}}{{{\nu _2}}}\]\[{\nu _2} = {\nu _1}\frac{{{U_2}}}{{{U_1}}}\]\[{\nu _2} = 3000 \cdot \frac{{16}}{{24}} = 2000\;об/мин\]
КАК решить
Известно, что за 15,7 минут колесо машины сделало 1000 оборотов. С какой скоростью передвигается машина, если диаметр ее колеса равен 60см?
Да в принципе решается задача также:\[\upsilon = \frac{{\omega D}}{2}\]\[\omega = 2\pi \nu \]\[\nu = \frac{N}{t}\]В итоге получим:\[\upsilon = \frac{{\pi ND}}{t}\]\[\upsilon = \frac{{3,14 \cdot 1000 \cdot 0,6}}{{15,7 \cdot 60}} = 2\;м/с\]
Колеса поезда вращаются с частотой 480 об/мин. С некоторого момента времени поезд начинает тормозить и колеса вращаются равнозамедленно с угловым ускорением ?=4рад/с2. Рассчитать время остановки и число оборотов колеса до остановки.
\[t = \frac{{{\omega _0}}}{\varepsilon } = \frac{{2 \cdot 3,14 \cdot 8}}{4} = 4\pi = 12,56\;с\]Напомню, что 480 об/мин = 8 Гц\[\varphi = {\omega _0}t – \frac{{\varepsilon {t^2}}}{2} = \varepsilon {t^2} – \frac{{\varepsilon {t^2}}}{2} = \frac{{\varepsilon {t^2}}}{2}\]\[N = \frac{\varphi }{{2\pi }} = \frac{{\varepsilon {t^2}}}{{4\pi }}\]\[N = \frac{{4 \cdot {{\left( {4\pi } \right)}^2}}}{{4\pi }} = 16\pi = 50,24\]
а не легще например радиуш колеша 1000 оборотв 300 300 умножаем на 60 делим на 1000 вуалйа 18 км щаш извините клавиатура шломалащь
Может быть и “легще”, но я ничего не понял
Точка покрышки колеса автомобиля вращается с постоянной по модулю скоростью. За две минуты она совершила N=60 оборотов . T- время одного оборота. Радиус колеса равен 50 см. Вычислить скорость и период вращения точки.
\[T = \frac{t}{N} = \frac{{120}}{{60}} = 2\;с\]\[\upsilon = \omega R = \frac{{2\pi R}}{T} = \frac{{2 \cdot 3,14 \cdot 0,5}}{2} = 1,57\;м/с\]
Большое спасибо
автомобиль движется между городами “а” и “б” с постоянной скоростью 60 км/ч. Определить частоту вращения колеса автомобиля и сколько оборотов сделает каждое колесо в течении поездки, если расстояние между городами 180 км
Без известного радиуса колеса решить задачу не представляется возможным
Sattva, переведите скорость 18,37м/сек в км/час и получите те же самые 66,13 км/час
В системе СИ нет единиц измерения “сек”, “час”, пожалуйста, пишите для секунд – “с”, а для часов – “ч”.
как узнать скорость, если диаметр колеса 39 см, а скорость вращения 900 оборотов в секунду?
Таким же образом, используете такую же формулу:
v=3,14·900·0,39=1102,14 м/с
Вероятно скорость вращения все-таки 900 оборотов в минуту, иначе, как Вы видите, мы получаем невероятную скорость в 1,1 км/с. Если я прав, то ответ будет таким:
v=3,14·900/60·0,39=18,37 м/с
Есть ошибка с переводом единиц в систему Си.
v=3,14 * 900 (оборотов в минуту) * 0,39 (метра) = 1102,14 м/мин
Именно метра в минуту.
Не может быть 1102,14 м/с, если у нас вращение
900 оборотов в минуту.
Далее 1102,14 м/мин =
1102,14 * 60 минут / 1000 метров = 66,13 км/час
Вывод: при размере колеса в 39 см (15,35 дюймов) и скорости вращения 900 об/мин,
объект (автомобиль) двигается с нормальной скоростью 66,13 км/час.
Никак не с космической скоростью в 1,1 км/сек.
Это неверно.