icodepro.ruУсловие задачи:
Обруч катится по горизонтальной плоскости без проскальзывания со скоростью \(\upsilon\). Чему равен модуль скорости верхней точки относительно поверхности Земли?
Задача №1.8.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon\), \(\upsilon_{в}-?\)
Решение задачи:
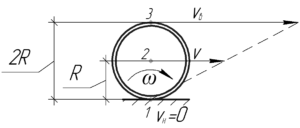Движение обруча по Земле называется качением, это особый случай движения, при котором каждая точка обруча одновременно и вращается вокруг своей оси, и движется поступательно (так называемое плоскопараллельное движение). При таком движении (плоскопараллельном) всегда имеется точка, скорость которой равна нулю. Если обруч движется без проскальзывания, то такой точкой является точка касания обруча с Землей (точка 1 на рисунке). Эту точку также называют мгновенным центром скоростей (МЦС). В каждый момент времени все точки колеса совершают вращательное движение вокруг МЦС, естественно, с одинаковой угловой скоростью \(\omega\).
Расстояние от точки на оси обруча (точка 2) до МЦС равно радиусу обруча \(R\), до верхней точки (точка 3) – \(2R\), поэтому:
\[\left\{ \begin{gathered}
\upsilon = \omega \cdot R \hfill \\
{\upsilon _в} = \omega \cdot 2R \hfill \\
\end{gathered} \right.\]
Делим выражения системы друг на друга:
\[\frac{{{\upsilon _в}}}{\upsilon } = 2 \Rightarrow {\upsilon _1} = 2\upsilon \]
Ответ: \(2\upsilon\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.8.20 Найти радиус вращающегося колеса, если линейная скорость точки на ободе
1.8.22 Точки окружности вращающегося диска имеют линейную скорость по модулю
1.8.23 Угловая скорость лопастей вентилятора 20pi рад/с. Найти число оборотов
