Определите время равноускоренного движения снаряда в стволе длиной 3 м

Условие задачи:

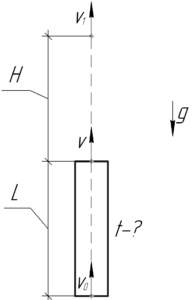
Определите время равноускоренного движения снаряда в стволе длиной 3 м вертикально установленного орудия, если после выстрела снаряд достигает высоты 4500 м.

Задача №1.4.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=3\) м, \(H=4500\) м, \(t-?\)

Решение задачи:

Так как после вылета из ствола орудия снаряд достигает максимальной высоты \(H\), то возможно найти скорость снаряда \(\upsilon\) при вылете по формуле:

\[\upsilon _1^2 – {\upsilon ^2} =  – 2gH\]

Понятно, что на высоте \(H\) скорость тела \(\upsilon_1\) равна нулю, поэтому:

\[{\upsilon ^2} = 2gH\]

\[\upsilon  = \sqrt {2gH} \;\;\;\;(1)\]

Теперь применим ту же формулу, но для участка равноускоренного движения снаряда в стволе пушки.

\[{\upsilon ^2} – \upsilon _0^2 = 2aL\]

Понятно, что начальная скорость снаряда \(\upsilon_0\) равна нулю. Также скажу о том, что в этой формуле \(a\) – это ускорение снаряда, по сути векторная сумма ускорений, создаваемых давлением пороховых газов и силой тяжести. Тогда:

\[{\upsilon ^2} = 2aL\;\;\;\;(2)\]

Так как движение снаряда в стволе равноускоренное, то запишем формулу определение ускорения:

\[a = \frac{{\upsilon  – {\upsilon _0}}}{t} = \frac{\upsilon }{t}\;\;\;\;(3)\]

Подставим (3) в (2) и выразим искомое время \(t\):

\[{\upsilon ^2} = 2\frac{\upsilon }{t}L \Rightarrow \upsilon  = \frac{{2L}}{t} \Rightarrow t = \frac{{2L}}{\upsilon }\]

Подставим в полученное выражение формулу (1) и будем иметь конечную формулу.

\[t = \frac{{2L}}{{\sqrt {2gH} }}\]

\[t = \frac{{2 \cdot 3}}{{\sqrt {2 \cdot 10 \cdot 4500} }} = 0,02\; с = 20\; мс\]

Ответ: 20 мс.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.4.22 Тело, брошенное вертикально вверх, за третью секунду прошло 5 м. Определить
1.4.24 При равноускоренном движении тело проходит за четвертую секунду 16 м. Определить
1.4.25 С вертолета, находящегося на высоте 500 м, упал камень. Через какое время