Условие задачи:

Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно земли равна 3 м/с?

Задача №1.7.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$\upsilon_1=4$ м/с, $\upsilon_0=3$ м/с, $\upsilon-?$

Решение задачи:

Так как в безветренную погоду воздух неподвижен, то скорость $\upsilon_1$ — это скорость не только относительно земли, но и относительно воздуха.

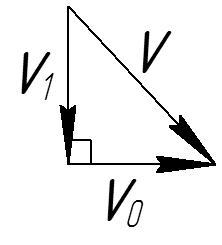
Скорость парашютиста при наличии ветра определяется правилом сложения скоростей. Вектор его скорости относительно земли $\overrightarrow \upsilon$ есть сумма вектора скорости движения относительно воздуха $\overrightarrow {{\upsilon _1}}$ и вектора скорости ветра $\overrightarrow {{\upsilon _0}}$.

$$\overrightarrow \upsilon   = \overrightarrow {{\upsilon _1}}  + \overrightarrow {{\upsilon _0}}$$

Так как человек с парашютом падает вертикально вниз (относительно воздуха), а ветер дует горизонтально, то угол между векторами $\overrightarrow {{\upsilon _1}}$ и $\overrightarrow {{\upsilon _0}}$ — прямой. Применим теорему Пифагора:

$${\upsilon ^2} = \upsilon _1^2 + \upsilon _0^2$$

$$\upsilon  = \sqrt {\upsilon _1^2 + \upsilon _0^2}$$

Сосчитаем ответ:

$$\upsilon  = \sqrt {{4^2} + {3^2}}  = 5\; м/с = 18\; км/ч$$

Ответ: 18 км/ч.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

1.7.18 Пассажирский поезд идет со скоростью 72 км/ч. По соседнему пути движется
1.7.20 Вертолет летит на высоте 500 м со скоростью 100 м/с. Навстречу ему по реке
1.7.21 В момент, когда тронулся поезд, провожающий стал равномерно бежать по ходу поезда